


Next: MC480 Mathematics Project
Up: Year 4
Previous: MC442 Differential Geometry
MC 445 Ring Theory
| Credits: 20 |
Convenor: Dr. J.F. Watters |
Semester: 2
|
| Prerequisites: |
essential: MC242 or MC341; MC249 or MC344=MC382 |
|
| Assessment: |
Continual assessment: 10% |
Three hour exam in May/June: 90% |
| Lectures: |
36 |
Classes: |
10 |
| Tutorials: |
none |
Private Study: |
104 |
| Labs: |
none |
Seminars: |
none |
| Project: |
none |
Other: |
none |
| Total: |
150 |
|
|
Explanation of Pre-requisites
It is desirable that students have experience of group theory and elementary
ring theory before taking this module. Group theory will have given
experience of working with cosets and factor groups and, if the Level 3
module has been studied, knowledge of isomorphism theorems. The
rings/abstract algebra modules include basic material on rings and ideals
which will be revised at the start of this module.
Course Description
The course explores the theme of structure in non-commutative rings. By
structure we mean being able to build rings from what we regard as
concrete examples using some tangible process. The process we use here is
the algebraic version of the Cartesian product, called the direct sum,
and the concrete examples are
matrix rings. The entries in these matrix rings have to be allowed to come not
merely from fields, but the non-commutative analogue, division rings.
In this course we explore the conditions we need to impose on a ring in
order that it be expressible as a direct sum of a finite number of matrix
rings over division rings. The conditions needed embody finiteness in a
certain way and also require the ring to be free of ideals of a particular
type. The division rings arise by considering simple modules; the
awkward ideals which we wish to be free of determine the Jacobson
radical; and the finiteness condition is imposed on descending chains of
ideals.
Aims
To develop the basic theory of modules over rings
leading to an understanding of the structure of certain classes of
non-commutative rings.
Objectives
To be familiar with the basic algebra of modules and rings.
To understand the direct sum construction.
To connect simple modules and division rings through Schur's Lemma.
To know the elementary properties of Artinian modules.
To define the prime and Jacobson radicals in rings.
To establish properties of these two radicals.
To prove the Wedderburn-Artin Theorem.
Transferable Skills
Developing understanding of abstraction and algebraic structure.
Ability to connect module concepts with ring concepts.
Understanding of proofs.
Ability to apply theorems to solve problems.
Written presentation of algebraic arguments.
Syllabus
Rings, ideals and homomorphisms.
Modules; submodules, factor modules and homomorphisms; cyclic, simple and
semisimple modules;
(if time; free, projective, and injective module).
Finiteness conditions on rings and modules.
Simple, prime, and primitive rings.
The prime radical.
The Jacobson radical.
Structure of semi-simple rings.
Reading list
Recommended:
T.W. Hungerford,
Algebra,
Springer, 1984.
N.H. McCoy,
The Theory of Rings,
Macmillan, 1964.
Background:
Details of Assessment
Coursework will be set weekly and marks gained will provide the coursework
component for the assessment 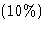 . The midsummer examination will be of
three hours duration. It will contain 6 questions with full marks attainable
for complete answers to 4 questions. The examination mark gives
. The midsummer examination will be of
three hours duration. It will contain 6 questions with full marks attainable
for complete answers to 4 questions. The examination mark gives 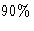 of the assessment for the
module.
of the assessment for the
module.



Next: MC480 Mathematics Project
Up: Year 4
Previous: MC442 Differential Geometry
S. J. Ambler
11/20/1999