


Next: MC445 Ring Theory
Up: Year 4
Previous: MC435 General Relativity
MC442 Differential Geometry
| Credits: 20 |
Convenor: Dr. J. Hunton |
Semester: 1 |
| Prerequisites: |
essential: MC240, MC241, MC224 |
|
| Assessment: |
Individual and group coursework: 15% |
Three hour examination in January: 85% |
| Lectures: |
32 |
Classes: |
10 |
| Tutorials: |
none |
Private Study: |
104 |
| Labs: |
none |
Seminars: |
4 |
| Project: |
none |
Other: |
none |
| Total: |
150 |
|
|
Explanation of Pre-requisites
This module will draw on some basic ideas from both algebra and analysis. Some
facility with basic skills from linear algebra and both single and
multivaraible calculus will be assumed. While this module is not a
prerequisite for MC435 General Relativity, it may provide helpful background
ideas.
Course Description
The Earth is round, but maps are drawn on flat pieces of paper. When the map is
only a street plan of a city this doesn't matter much, but when the map is of a
whole country there can be big discrepancies between the real geography and
what
the map appears to describe. In a similar manner, Einstein's theory of General
Relativity tells us that the Universe is curved, but it's much easier to do the
mathematics describing processes in physics as if, at least in local regions,
the Universe was flat. The questions of how can we reconcile our ability to do
mathematics (drawing curves, measuring distances, differentiating functions and
so on) on flat surfaces and spaces with our need to deal with undulating land
and curved space-time form the basis of Differential Geometry.
This is an introductory course and will concentrate on presenting some of the
ideas of the subject through a study of low dimensional questions and simple
geometric objects. It will begin with the study of the most simple geometric
examples, namely curves in the plane, and will then proceed to elaborate the
ideas needed for studying those to examine more complicated geometric
entities. We will see that at each stage we can abstract and generalise the
concepts we used before to the next level of complexity, thus the module ought
to `reinforce' itself as we go along: the same ideas will keep cropping up
again
and again.
There will be a group project which will involve applying the concepts of the
module to the mathematics of map-making (cartography).
Aims
The aim of this module is to introduce understanding of some of the
methods, scope and results of Differential Geometry through a study of low
dimensional questions and simple geometric objects. The module also aims to
teach some of the subject's applications to cartography and
know some of the geometric language that is utilised in other areas of science
such as General Relativity. Additionally, the module demonstrates a process
of mathematical abstraction and development.
Objectives
To know the definitions of and understand the key concepts introduced in this
module.
To be able to understand, reproduce and apply the main results and proofs in
this module.
To be able to solve routine problems in the subject matter covered.
To be aware of some of the applications of the subject.
To give the opportunity for participation in a group project and presentation.
Transferable Skills
The ability to present arguments and solutions in a coherent and logical form.
The ability to use the techniques taught within the module to solve problems.
Improved ability in group work and presentation skills.
Syllabus
After about three or four introductory lectures explaining
the nature of the module and the subject matter, the module
splits into four main sections.
§1 Smooth curves in 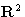 . Definition of
smooth, regular curves in
. Definition of
smooth, regular curves in 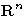 with notions of speed and arc
length parametrisation. For curves in
with notions of speed and arc
length parametrisation. For curves in 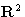 the necessary
apparatus (signed curvature) to prove the Fundamental Theorem
classifying such objects. Examples.
§2 Smooth curves in
the necessary
apparatus (signed curvature) to prove the Fundamental Theorem
classifying such objects. Examples.
§2 Smooth curves in 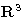 . Frenet-Serret
apparatus and equations and proof of the Fundamental Theorem for
curves in
. Frenet-Serret
apparatus and equations and proof of the Fundamental Theorem for
curves in 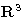 . Examples. Geometric interpretation of torsion.
§3 Surfaces in
. Examples. Geometric interpretation of torsion.
§3 Surfaces in 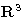 . Definition of
smooth surfaces, tangent planes and normals in
. Definition of
smooth surfaces, tangent planes and normals in 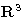 .Orientability. The first fundamental form and computations of arc
length, angle and area on a surface. Curvature and Gauss's proof of
Euler's theorem on principal curvatures. Computations and examples.
Isometries.
§4 Surfaces not in
.Orientability. The first fundamental form and computations of arc
length, angle and area on a surface. Curvature and Gauss's proof of
Euler's theorem on principal curvatures. Computations and examples.
Isometries.
§4 Surfaces not in 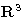 . Abstract
manifolds, bundles, tangents. Partitions of unity and metrics.
Group Project. Elementary mathematical cartography.
. Abstract
manifolds, bundles, tangents. Partitions of unity and metrics.
Group Project. Elementary mathematical cartography.
Reading list
Recommended:
John McCleary,
Geometry from a Differential Viewpoint,
Cambridge University Press.
Background:
William Boothby,
An introduction to Differentiable
Manifolds and Riemannian Geometry,
Academic Press.
Th. Bröcker and K. Jänich,
Introduction to Differential Topology,
Cambridge University Press.
M. Spivak,
A Comprehensive Introduction to
Differential Geometry,
Publish or Perish.
Details of Assessment
There will be a series of pieces of work set during the semester which together
will count for 10% of the final mark. There will be a short group project on
aspects of the module run part way through the semester which will count for
5% of the final mark.
There will be six questions on the examination paper; any number of questions
may be attempted but full marks may be gained from answers to four questions.
All questions will carry equal weight. The examination will be worth 85% of
the final mark.



Next: MC445 Ring Theory
Up: Year 4
Previous: MC435 General Relativity
S. J. Ambler
11/20/1999