


Next: MC341 Group Theory
Up: Year 3
Previous: MC323 Ordinary Differential Equations
MC340 Number Theory
| Credits: 20 |
Convenor: Dr. G. Rousseau |
Semester: 1 |
| Prerequisites: |
|
|
| Assessment: |
Continuous assessment: 10% |
Three hour exam in January: 90% |
| Lectures: |
36 |
Classes: |
12 |
| Tutorials: |
none |
Private Study: |
92 |
| Labs: |
10 |
Seminars: |
none |
| Project: |
none |
Other: |
none |
| Total: |
150 |
|
|
Explanation of Pre-requisites
There are no specific pre-requisites, though some familiarity with
the most basic concepts of algebra is desirable.
Course Description
The module provides an introduction to the study of properties of the natural
numbers which have exercised the imagination of mathematicians
and amateurs from antiquity to the present day.
After a discussion of linear congruences and their solution and of systems of
linear equations and their solution in integers, attention will be turned to
Gauss's theory of quadratic congruences and quadratic forms, and results
will be derived concerning the representation of positive integers
as sums of squares.
Aims
The course aims to introduce the basic concepts of elementary number theory
and to provide the student with an understanding of these.
Transferable Skills
The student will gain facility with linear and quadratic congruences, the
conditions for their solvability, on the one hand,
and their practical solution on the other.
Similarly, the student will gain the
ability to determine solvability of indeterminate equations in integers
(linear and quadratic) and to solve them practically.
Syllabus
:
Basic properties.
The Euclidean property.
Quotient and remainder.
Greatest common divisor.
Euclid's algorithm.
Calculating g.c.d.
Relatively prime numbers.
G.c.d. of several numbers.
Relatively prime and pairwise relatively prime.
Prime and composite.
Representability as products of primes.
Existence of infinitely many primes.
Euclid's Lemma - if a prime number divides a product then it must divide
one of the factors.
Fundamental theorem of arithmetic.
Consequences.
Least common multiple.
The number-of-divisors function.
The sum-of-divisors function.
Euler's phi-function.
Multiplicative functions.
:
Basic properties.
Cancellation laws.
Linear congruences.
Practical methods of solution.
Condition for solvability.
Number of solutions.
Simultaneous congruences.
Chinese Remainder Theorem.
Residue classes.
Residue class rings.
Rings, integral domains, fields.
Zm is a field resp. integral domain iff m is prime.
Fermat's Theorem.
Proofs by Lagrange's subgroup theorem and binomial theorem.
Wilson's Theorem.
Euler's generalisation of Fermat's Theorem.
Quadratic congruences.
Reduction to prime power modulus, then to prime modulus.
Reduction to a binomial congruence by completing the square.
Lagrange's Theorem on number of roots.
Order of an element.
Primitive roots.
Existence.
Indices.
Solution of linear, quadratic and exponential congruences by the
method of indices.
Quadratic residues.
Even index criterion.
Euler's criterion.
The Jacobi symbol - Zolotarev-Frobenius definition.
Zolotarev's Theorem.
First and second congruence property.
First and second multiplicativity property.
First and second supplementary law.
The quadratic reciprocity law.
Calculating the Jacobi symbol.
Solubility of quadratic congruences to arbitrary moduli.
Determining the primes
of which a given integer is a quadratic residue.
Equations:
Linear diophantine equations.
Solution method for two variables.
The recurrence relations.
General solution.
Solutions in positive integers.
Equations in three variables.
Solving m equations in n unknowns.
Continued fractions.
Continued fraction expansion of a real number.
Convergents.
Uniqueness of continued fraction expansion.
Quadratic irrationals.
Lagrange's Theorem on the
periodicity of the continued fraction expansions of quadratic irrationals.
Solution of Pell's equation 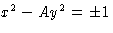 .
General solution.
Pythagorean triples.
Primitive Pythagorean triples.
Formula for primitive triples.
General solution of x2 + y2 = z2.
The case n=4 of Fermat's Last Theorem.
.
General solution.
Pythagorean triples.
Primitive Pythagorean triples.
Formula for primitive triples.
General solution of x2 + y2 = z2.
The case n=4 of Fermat's Last Theorem.
Forms:
Binary quadratic forms.
Representation of integers by a quadratic form.
Unimodular transformations.
Equivalence of quadratic forms.
Classes of equivalent forms.
Behaviour of coefficients under transformation.
Matrix formulation.
Discriminant of a form.
Positive definite forms.
Reduction of positive definite forms.
Semi-reduced and reduced forms.
The theorem that every
positive definite form is equivalent to a reduced form.
Class number.
Finiteness of the class number.
Finding all reduced forms with given discriminant.
Principal form.
Representation of integers by positive definite forms.
Proper representability.
Congruence criterion for proper representability.
Discriminants with class number 1.
Fermat's two-square theorem.
Girard's Theorem.
Reading list
Recommended:
H. Davenport,
The Higher Arithmetic,
Cambridge University Press.
A. Baker,
A Concise Introduction to Number Theory,
Cambridge University Press.
G. Rousseau,
Introduction to the Theory of Numbers,
Diophantos 1998.
Details of Assessment
The coursework for the continuous assessment consists of four tests,
at two-week intervals, starting approximately one month after the
beginning of the semester.
The January written examination consists of
eight questions of which five are to be attempted.



Next: MC341 Group Theory
Up: Year 3
Previous: MC323 Ordinary Differential Equations
Roy L. Crole
10/22/1998