Next: MC341 Group Theory
Up: Year 3
Previous: MC316 Parallel and Distributed
MC320 Modelling Biological Systems
| Credits: 20 |
Convenor: Dr. M. Walmsley |
Semester: 1 |
| Prerequisites: |
essential: MC120, MC121, MC144, MC145, MC146, MC147, MC248 |
|
| Assessment: |
Coursework: 10% |
Three hour exam: 90% |
| Lectures: |
36 |
Classes: |
10 |
| Tutorials: |
none |
Private Study: |
104 |
| Labs: |
none |
Seminars: |
none |
| Project: |
none |
Other: |
none |
| Total: |
150 |
|
|
Explanation of Pre-requisites
The module requires a general mathematical background, with some knowledge
of the use of Maple.
Course Description
This module uses differential equations of various kinds to describe certain
problems in the biological sciences. There are particular applications to
population models (including interaction between species) and epidemic
models. Some new techniques concerned with coupled differential equations
and partial differential equations are introduced.
Aims
The module will investigate a range of biological problems using modern
mathematical tools. The aim is to indicate the applicability of mathematics
to recent work in the life sciences.
Objectives
To be able to integrate simple ordinary differential equations, determine
their steady states and discuss the nature of their stability.
To be able to sketch direction fields and typical solutions and make
appropriate deductions concerning the biological problem under discussion.
To know how to introduce dimensionless variables.
To be able to use linear and nonlinear differential equations (usually
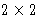, but possibly more when discussing epidemics) to describe a
given biological problem.
To know how to use the theory for 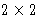autonomous systems (eigenvalues,
trace and determinant of Jacobian) to determine the character of steady
state solutions.
To be able to investigate the behaviour of solutions of differential equations
using standard MAPLE routines to obtain direction fields and phase portraits.
To be able to make deductions concerning the biological problem from the
mathematical results.
To know how to derive the diffusion equation in one and three dimensions.
To be familiar with the elementary solution and the error function solution
of the 1D diffusion equation.
To be able to use solutions of the diffusion equation in modelling
particular problems.
Transferable Skills
Mathematical modelling and problem solving skills, including the use of
differential equations routines in Maple.
Syllabus
- 1.
- Single species population models -- deterministic models.
- 2.
- Phase-plane methods and qualitative solutions of systems of ordinary differential
equations, with applications to predator-prey models, the Lotka-Volterra equations, the
population biology of infectious diseases. Maple provides suitable tools for the investigation
of problems arising in this area.
- 3.
- Introduction to the diffusion equation and its solution with applications
to particular problems.
Reading list
Background:
M.Braun,
Differential Equations and Their Applications,
Springer.
E. Renshaw,
Modelling Biological Populations in Space
and Time,
CUP.
J. D. Murray,
Mathematical Biology,
Springer
There is no single textbook for the course and
students will be referred to the above
relevant texts where appropriate; for example, Braun
discusses Phase-plane methods, and
Renshaw includes items of interest. Murray
is an advanced
textbook, small parts of which are relevant to the course.
All books are available in the library.
Details of Assessment
The final assessment of this module will consist of 10% coursework
and 90% from a three hour examination during the January exam
period. The 10% coursework contribution will be determined by students'
solutions to coursework problems. The examination paper will contain
6 questions with full marks on the paper obtainable from 4 complete answers.
Next: MC341 Group Theory
Up: Year 3
Previous: MC316 Parallel and Distributed
S. J. Ambler
11/20/1999