MC226 Numerical Linear Algebra

Next: MC227 Fluids and Waves Up: Year 2 Previous: MC224 Vector Calculus

MC226 Numerical Linear Algebra

Credits: 10

Convenor: Prof. B. Leimkuhler

Semester: 2

Prerequisites:	essential: MC146, MC147
Assessment:	Coursework: 20%	One and a half hour exam: 80%

Lectures:	18	Classes:	5
Tutorials:	none	Private Study:	47
Labs:	5	Seminars:	none
Project:	none	Other:	none
Total:	75

Explanation of Pre-requisites

All the material in the course MC147 (Introductory Linear Algebra) will be absolutely essential for this module. From the module MC146, the idea of a supremum will be required, as well as the material on convergence of sequences and the Intermediate Value Theorem.

Course Description

Solving linear systems Ax = b or finding the eigenvalues of a matrix may appear to be trivial tasks.

In fact, the systems of linear equations which arise in applications are often large, involving thousands or even millions of unknowns, and may be ill-conditioned (the solution may be very sensitive to the value of the right hand side). It is often then necessary to use an iterative method, which generates a sequence of approximations to the solution of the system. The rate of convergence of this sequence is very important.

For finding eigenvalues, even of a symmetric real matrix, it is certainly not feasible to locate the zeroes of the polynomial 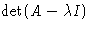$\det (A-\lambda I)$ :the work involved in doing this would be of the order of n! for an 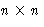$n\times n$ matrix A. Instead there are transformations which can be used to reduce the matrix to a simpler form, and these may be used in conjunction with an iterative or other method to locate the eigenvalues.

This course will describe some of these algorithms, which lie behind the methods used by many linear algebra software packages.

Aims

This course will present the mathematical algorithms and analysis behind software for numerical solution of linear systems of equations and matrix eigenvalue problems.

Objectives

By the end of this module a diligent student should be able to

form the LU and/or LL^T decompositions of appropriate matrices, and prove theorems on their existence under suitable hypotheses;
know how to define the Jacobi, Gauss-Seidel and SOR iterative schemes for solving linear systems; state and prove theorems on the circumstances in which these methods may be expected to converge;
prove the convergence of the power method and its variants for finding the eigenvalues of appropriate matrices; use the Sturm Sequence method for eigenvalues of tridiagonal matrices.

Transferable Skills

This course will impart a basic understanding of numerical linear algebra which is useful throughout science and engineering.

Syllabus

Gaussian Elimination; LU and Cholesky factorizations; Matrix norms; Iterative methods for linear equations, including Jacobi, Gauss-Seidel and Successive Over-Relaxation.

The Schur Decomposition; the Power method and its variants; the Sturm Sequence method for tridiagonal matrix eigenproblems; Householder transformations for tridiagonalisation of a symmetric matrix (if time allows).

Reading list

Details of Assessment

The final assessment of this module will consist of 10% coursework, 10% from a short series of MATLAB projects and 80% from a one and a half hour examination during the Summer exam period. The 10% coursework contribution will be determined by students' solutions to coursework problems. The examination paper will contain 4 questions with full marks on the paper obtainable from 3 complete answers.

Next: MC227 Fluids and Waves Up: Year 2 Previous: MC224 Vector Calculus

S. J. Ambler
11/20/1999