MC224 Vector Calculus

Next: MC226 Numerical Linear Algebra Up: Year 2 Previous: MC223 Relativity

MC224 Vector Calculus

Credits: 10

Convenor: Dr. M. Walmsley

Semester: 1 (weeks 1 to 6)

Prerequisites:	essential: MC125, MC126	desirable: MC144, MC145, MC146, MC147
Assessment:	Coursework: 20%	One and a half hour exam: 80%

Lectures:	18	Classes:	5
Tutorials:	none	Private Study:	52
Labs:	none	Seminars:	none
Project:	none	Other:	none
Total:	75

Explanation of Pre-requisites

The work on vectors, curves, partial differentiation and multiple integrals, which was covered in MC126, will form a basis for this module. A general mathematical knowledge from other modules is also required.

Course Description

This module will extend the vector algebra of the first year to the calculus of three dimensional vectors. This is an essential module for those wishing to take certain later modules in Applied Mathematics, for example Fluids and Waves, General Relativity, Electromagnetic Theory etc.

Aims

The use of vectors simplifies and condenses the mathematical discussion of many problems which arise in applied mathematics and so this module forms a basis for many later modules. However, vector calculus may be studied in its own right and here links with multivariable analysis will be apparent.

Objectives

To be familiar with scalar, vector and triple products and their use in the description of lines and planes.

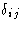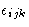To be familiar with the use of the summation convention including the Kronecker delta $\delta_{ij}$ and the alternating tensor $\epsilon_{ijk}$ .

To know the definitions of, and to be able to use, the vector differential operators grad, div and curl, and the Laplacian.

To be able to work with line, surface and volume integrals.

To be able to state and use in simple cases Green's theorem in the plane, the divergence theorem and Stokes' theorem.

Transferable Skills

This module provides essential mathematics for any practising applied mathematician.

Syllabus

Introduction to vector algebra.

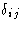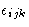Introduction of suffix notation and the summation convention including $\delta_{ij}$ and $\epsilon_{ijk}$ .

The vector differential operators grad, div and curl.

Line, surface and volume integrals with particular application to the divergence theorem and Stokes' theorem.

Reading list

Background:

M. R. Spiegel, Vector Analysis, Schaum Outline Series.

H. P. Hsu, Applied Vector Calculus, Harcourt Brace Jovanovich College Outline Series.

E. A. Maxwell, Coordinate Geometry with Vectors and Tensors, CUP? Probably out of print..

J. Gilbert, Guide to Mathematical Methods, MacMillan.

P.C. Matthews, Vector Calculus, Springer
There are in addition a number of Vector Analysis texts located at 515.63 in the Library.

Details of Assessment

There will be four pieces of work of equal weight set for assessment and these together count for 20% of the final mark. The examination paper contains four questions. Any number of questions may be attempted but only the best three answers will be taken into account. Full marks may be obtained for answers to three questions, and all questions carry equal weight.

Next: MC226 Numerical Linear Algebra Up: Year 2 Previous: MC223 Relativity

S. J. Ambler
11/20/1999