Next: MC148 Pure Mathematics at
Up: Year 1
Previous: MC146 Introductory Real Analysis
MC147 Introductory Linear Algebra
| Credits: 10 |
Convenor: Dr. B. Leimkuhler |
Semester: 2 |
| Prerequisites: |
essential: MC144, MC145 |
|
| Assessment: |
Coursework, Maple project: 20% |
One and a half hour exam: 80% |
| Lectures: |
18 |
Classes: |
none |
| Tutorials: |
5 |
Private Study: |
46 |
| Labs: |
6 |
Seminars: |
none |
| Project: |
none |
Other: |
none |
| Total: |
75 |
|
|
Explanation of Pre-requisites
The modules MC144 and MC145 provide the axiomatic experience on which
this module builds. The concept of a field, introduced in MC145, is used in
defining an abstract vector space. MC145 also provides the introduction to
Maple which is used in this module.
Course Description
Vector spaces arise in many areas of mathematics. This course begins
by defining vector spaces over a field and introduces the ideas which
lead to the concept of dimension. Dimension depends on the
notion of a basis, and to identify a basis we need to be able to solve systems
of linear equations. This course explores how to solve such systems by a
methodical use of matrices and elementary row operations. The course concludes with
an introduction to eigenvalues and eigenvectors of matrices for which we need
to provide some basic material on determinants. Maple laboratories run for
about six weeks to support the lectures.
Aims
This module introduces abstract vector spaces and the concepts of linear
independence, spanning, bases and dimension. Techniques for solving
systems of linear equations, the theory underpinning these techniques, and the
role of matrices in such problems are presented. The module also aims to
provide some facility in finding eigenvalues and eigenvectors of matrices.
Maple is used alongside the lectures to provide both pedagogical support and
to show how a number of the tasks of linear algebra can be carried out by Maple.
Material taught in this module provides the necessary foundation for the
continued treatment of abstract vector spaces in MC241.
Objectives
To understand the definition and fundamental examples of vector spaces and
subspaces; to be able to verify that certain subsets of vector spaces are
subspaces; to understand the ideas of a linear combination of vectors, the
space spanned by a set of vectors, linear independence, basis and dimension;
to be able to find a basis for the space spanned by a given set of vectors.
To understand how to use elementary row operations on matrices to solve systems
of linear equations; to know how to use Maple to carry out these computations;
to understand the role of the rank and the row-reduced echelon form; to
understand the varying nature of solution sets.
To be able to perform the operations of matrix algebra, including finding
determinants and inverses; to know how to use Maple to carry out such tasks.
To be able to compute the eigenvalues and eigenvectors of a matrix; to know
how to diagonalise matrices in simple cases.
Transferable Skills
An understanding of abstraction and the axiomatic method.
The ability to solve systems of linear equations methodically.
The ability to perform matrix computations including diagonalisation.
Knowledge of Maple as a tool for doing linear algebra.
The ability to present logical arguments in written form.
Syllabus
Definition of a vector space over a field F, fundamental examples of
vector spaces, elementary consequences of the definition, subspaces,
intersections of subspaces, linear combinations of vectors, the space
spanned by a set of vectors, linear independence, basis, dimension, the
exchange process
Homogeneous and inhomogeneous systems of linear equations, the matrix
form of a system of linear equations, elementary row operations, Gaussian
elimination, row equivalence, row-reduced echelon form of a matrix, rank
of a matrix, parametric and non-parametric descriptions of the space
spanned by a set of vectors in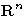 
, row space and row rank,
column space and column rank, null space and nullity
Addition and multiplication of matrices, invertibility, using row operations
to find the inverse of an invertible matrix, elementary matrices, rank and
invertibility, cofactors and minors of a matrix, determinants, the determinant
of a product, the adjoint of a matrix
Eigenvalues, eigenvectors, the characteristic polynomial and characteristic
equation of a matrix, similarity of matrices, diagonalisation, the
Cayley-Hamilton Theorem, powers of a matrix
Reading list
Recommended:
R. B. J. T. Allenby,
Linear Algebra,
Edward Arnold, 1995.
J. B. Fraleigh and R. A. Beauregard,
Linear Algebra, 3rd edition,
Addision-Wesley, 1995.
L. W. Johnson, R. P. Riess, and J. T. Arnold,
Introduction to Linear Algebra, 3rd edition,
Addison-Wesley, 1993.
G. Strang,
Linear Algebra and its Applications, 3rd edition,
Harcourt Brace Jovanovich, 1988.
Background:
S. Lipschutz,
Schaum's Outline of Theory and Problems of Linear Algebra, 2nd edition,
McGraw-Hill, 1991.
Details of Assessment
Details of Assessment
The final assessment of this module will consist of 10% coursework, 10%
from a MAPLE project and 80% from a one and a half hour examination during
the Summer exam period. The 10% coursework contribution will be determined
by students' solutions to coursework problems. The examination paper will contain
4 questions with full marks on the paper obtainable from 4 complete answers.
Next: MC148 Pure Mathematics at
Up: Year 1
Previous: MC146 Introductory Real Analysis
S. J. Ambler
11/20/1999