MC146 Introductory Real Analysis

Next: MC147 Introductory Linear Algebra Up: Year 1 Previous: MC145 Algebraic Structures and

MC146 Introductory Real Analysis

Credits: 10

Convenor: Dr. M. Marletta

Semester: 2

Prerequisites:	essential: MC144, MC145
Assessment:	Coursework and tests: 20%	One and a half hour examination: 80%

Lectures:	18	Classes:	none
Tutorials:	5	Private Study:	52
Labs:	none	Seminars:	none
Project:	none	Other:	none
Total:	75

Explanation of Pre-requisites

This module continues the discussion of number systems from MC145; in particular, familiarity with the rational numbers will be assumed. The module will contain rigorous mathematical discussion of the central concepts and so will draw on the notions of proof and logical argument introduced in MC144 and applied in MC145. Familiarity with the idea of a function, as introduced in these previous modules, will also be important.

Course Description

This course will introduce students to the beginnings of Real Analysis, the study of the mathematics of the continuous number line. For a variety of reasons, it turns out that there are not enough rational numbers; for example, as 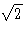$\sqrt{2}$ is not a rational, the equation x²-2=0 has no solution in the rational numbers, equivalently, there is no rational point at which the graph of the function y=x²-2 crosses the x-axis. To remedy this situation the real numbers are invented, but that leads to questions such as `how do you actually define the real numbers?', `how do you know when you have defined enough real numbers?' and `how do the real numbers differ from the rational numbers?' This module attempts to answer these questions.

Aims

This module aims to introduce the basic ideas of mathematical analysis and to familiarise students with the elementary properties of the real numbers and of the concepts of continuity, sequences and limits.

Objectives

To know the definitions of and understand the key concepts introduced in this module.

To be able to understand, reproduce and apply the main results and proofs in this module.

To understand the difference between the real and rational numbers.

To be able to solve routine problems on the continuity of functions, the convergence of sequences, the existence of limits of functions and on the differentiability of functions.

Transferable Skills

The ability to present arguments and solutions in a coherent and logical form.

Syllabus

Questions of the nature of the real numbers and how they differ from the rationals. Motivation for the module from a discussion of the intermediate value theorem as intuitively obvious but nevertheless failing for the rationals.

Continuity via 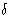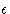$\delta$ , $\epsilon$ language. Examples, with full proof, of continuous and of non-continuous functions. Proof of continuity of sums, products and composites of continuous functions; continuity of polynomial functions.

Definition of supremum and examples. Proofs of basic properties of suprema. Statement of the completion property of the reals. Proof of the intermediate value theorem. Infima as `dual' ideas to those concerning suprema. Sketch construction of the real numbers (Dedekind cuts).

Concept of a sequence and the notion of convergence to a limit. Examples. Proof of results on sums, products and quotients of convergent sequences. Proof of monotone convergence theorems. Applications to computations of limits of sequences defined by rational polynomials and by inductive formulæ. Second sketch construction of the real numbers (equivalence classes of monotone increasing, bounded above sequences).

The limit of a function; continuity via limits. Proof of the equivalence between the limit definition of continuity and the 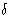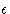$\delta$ , $\epsilon$ version. Application to reproving results on sums and products of continuous functions from the work on sequences. Examples (with proofs) of functions having or not having limits at certain points.

Application of the idea of limit to rigorous definition of differentiablity. Proof of differentiablity of polynomial functions, via that of sums, products etc. Examples (with proofs) of functions differentiable or not differentiable at certain points. Proof that differentiable implies continuous.

Reading list

Background:

T. M. Apostol, Mathematical Analysis, Addison-Wesley.

K. G. Binmore, Mathematical Analysis, Cambridge.

J. C. Burkill, A First Course in Mathematical Analysis, Cambridge.

M. Hart, An Guide to Analysis, Macmillan.

J. B. Read, An Introduction to Mathematical Analysis, Oxford.

Details of Assessment

The final assessment of this module will consist of 20% coursework and 80% from a one and a half hour examination during the Summer exam period. The 20% coursework contribution will be determined by students' solutions to coursework problems. The examination paper will contain 4 questions with full marks on the paper obtainable from 4 complete answers.

Next: MC147 Introductory Linear Algebra Up: Year 1 Previous: MC145 Algebraic Structures and

S. J. Ambler
11/20/1999