![[The University of Leicester]](http://www.le.ac.uk/corporateid/departmentresource/000066/unilogo.gif) | Department of Mathematics |
 |
Next: MA4121 Projective Curves
Up: ModuleGuide03-04
Previous: MA4101 Algebraic Topology
MA4111 Differential Geometry
| Credits: 20 |
Convenor: Prof. J.R. Hunton |
Semester: 1 (weeks 1 to 12) |
| Prerequisites: |
essential: MA2002, MA2151 |
desirable: MA3151 |
| Assessment: |
Coursework: 15% |
Examination: 85% |
| Lectures: |
36 |
Problem Classes: |
6 |
| Tutorials: |
none |
Private Study: |
108 |
| Labs: |
none |
Seminars: |
none |
| Project: |
none |
Other: |
none |
| Surgeries: |
none |
Total: |
150 |
Subject Knowledge
Aims
The aim of this module is to introduce understanding of some of the
methods, scope and results of Differential Geometry through a study of low
dimensional questions and simple geometric objects. The module also aims to
teach some of the subject's applications to cartography and
know some of the geometric language that is utilised in other areas of science
such as General Relativity. Additionally, the module demonstrates a process
of mathematical abstraction and development.
Learning Outcomes
To know the definitions of and understand the key concepts of low
dimensional differnetial geometry as introduced in this module and to be
able to understand, reproduce and apply the main results and proofs
given. Students will also be able to solve routine problems in the
subject matter covered and be aware of some of the applications of the
subject.
Methods
Lectures, example classes, example sheets, group project.
Assessment
Marked problem sheets, written examination, group presentation.
Subject Skills
Aims
To see how one can extend classical `flat' mathematics to the
study of the geometry of curved objects (curves, surfaces, and so on). To
become more aware of the mathematical process of abstraction.
Learning Outcomes
Students will become familiar with the analysis of differentiable
curves, surfaces and their generalisation, and be aware of their
application to the mathematical theory of map making.
Methods
Lectures, examples classes, example sheets, group project.
Assessment
Marked problem sheets, written examination, group presentation.
Explanation of Pre-requisites
This module needs some knowledge of both analysis and the techniques of
vector or multivariate calculus. The analysis needed requires the student
to be comfortable with discussing reasonably straightforward topological
spaces such as curves, spheres, tori, discs and so on. Conceptually, this
is all more than covered in the Abstract Analysis course MA2151, but more
familiarity with these conceps will be gained from the Topology module
MA3151 which would be a good partner with this module.
Course Description
The Earth is round, but maps are drawn on flat pieces of paper. When the
map is only a street plan of a city this doesn't matter much, but when
the map is of a whole country there can be big discrepancies between the
real geography and what
the map appears to describe. In a similar manner, Einstein's theory of General
Relativity tells us that the Universe is curved, but it's much easier to do the
mathematics describing processes in physics as if, at least in local regions,
the Universe was flat. The questions of how can we reconcile our ability to do
mathematics (drawing curves, measuring distances, differentiating functions and
so on) on flat surfaces and spaces with our need to deal with undulating land
and curved space-time form the basis of Differential Geometry.
This is an introductory course and will concentrate on presenting some of the
ideas of the subject through a study of low dimensional questions and simple
geometric objects. It will begin with the study of the most simple geometric
examples, namely curves in the plane, and will then proceed to elaborate the
ideas needed for studying those to examine more complicated geometric
entities. We will see that at each stage we can abstract and generalise the
concepts we used before to the next level of complexity, thus the module ought
to `reinforce' itself as we go along: the same ideas will keep cropping up
again
and again.
There will be a group project which will involve applying the concepts of the
module to the mathematics of map-making (cartography).
Syllabus
After about three or four introductory lectures explaining
the nature of the module and the subject matter, the module
splits into four main sections.
§1 Smooth curves in 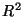 . Definition of
smooth, regular curves in
. Definition of
smooth, regular curves in 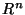 with notions of speed and arc
length parametrisation. For curves in
with notions of speed and arc
length parametrisation. For curves in 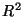 the necessary
apparatus (signed curvature) to prove the Fundamental Theorem
classifying such objects. Examples.
the necessary
apparatus (signed curvature) to prove the Fundamental Theorem
classifying such objects. Examples.
§2 Smooth curves in 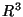 . Frenet-Serret
apparatus and equations and proof of the Fundamental Theorem for
curves in
. Frenet-Serret
apparatus and equations and proof of the Fundamental Theorem for
curves in 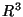 . Examples. Geometric interpretation of torsion.
. Examples. Geometric interpretation of torsion.
§3 Surfaces in 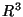 . Definition of
smooth surfaces, tangent planes and normals in
. Definition of
smooth surfaces, tangent planes and normals in 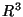 .
Orientability. The first fundamental form and computations of arc
length, angle and area on a surface. Curvature and Gauss's proof of
Euler's theorem on principal curvatures. Computations and examples.
Isometries.
.
Orientability. The first fundamental form and computations of arc
length, angle and area on a surface. Curvature and Gauss's proof of
Euler's theorem on principal curvatures. Computations and examples.
Isometries.
§4 Surfaces not in 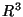 . Abstract
manifolds, bundles, tangents. Partitions of unity and metrics.
. Abstract
manifolds, bundles, tangents. Partitions of unity and metrics.
Group Project. Elementary mathematical cartography.
Reading list
Recommended:
John McCleary,
Geometry from a Differential Viewpoint,
Cambridge University Press.
Background:
William Boothby,
An introduction to Differentiable
Manifolds and Riemannian Geometry,
Academic Press.
Th. Bröcker and K. Jänich,
Introduction to Differential Topology,
Cambridge University Press.
M. Spivak,
A Comprehensive Introduction to
Differential Geometry,
Publish or Perish.
Resources
Problem sheets, lecture rooms, lecturer, cartographical handouts.
Module Evaluation
Module questionnaires, module review, year review.
Next: MA4121 Projective Curves
Up: ModuleGuide03-04
Previous: MA4101 Algebraic Topology
Author: C. D. Coman, tel: +44 (0)116 252 3902
Last updated: 2004-02-21
MCS Web Maintainer
This document has been approved by the Head of Department.
© University of Leicester.
![[The University of Leicester]](http://www.le.ac.uk/corporateid/departmentresource/000066/unilogo.gif)
![[The University of Leicester]](http://www.le.ac.uk/corporateid/departmentresource/000066/unilogo.gif)