![[The University of Leicester]](http://www.le.ac.uk/corporateid/departmentresource/000066/unilogo.gif) | Department of Mathematics |
 |
Next: MA4111 Differential Geometry
Up: ModuleGuide03-04
Previous: MA4041 Methods in Molecular Simulation
MA4101 Algebraic Topology
| Credits: 20 |
Convenor: Prof. J.R. Hunton |
Semester: 2 (weeks 15 to 26) |
| Prerequisites: |
essential: MA2102 or MA2111, MA2151 |
desirable: MA3151 |
| Assessment: |
Coursework: 10% |
Examination: 90% |
| Lectures: |
36 |
Problem Classes: |
6 |
| Tutorials: |
none |
Private Study: |
108 |
| Labs: |
none |
Seminars: |
none |
| Project: |
none |
Other: |
none |
| Surgeries: |
none |
Total: |
150 |
Subject Knowledge
Aims
This module aims to introduce the basic ideas of algebraic topology and to
demonstrate its power by proving some memorably entitled theorems.
Learning Outcomes
Students will understand some of the common processes of translating
topological or geometric infomation into algebraic information, seeing
examples of this through singular and simplicial homology. They will gain
some understanding of the language and techniques of category theory and
homological algebra. They will know some of the classical applications of
the algebraic topology such as the Ham Sandwich theorem, the Hairy Dog
theorem the Borsuk-Ulam theorem.
Methods
Lectures, example classes, example sheets.
Assessment
Marked problem sheets, written examination.
Subject Skills
Aims
To see how one can use a number of apparently distinct branches of
mathematics to solve new types of problem. To further increase
problem solving and written presentation skills.
Learning Outcomes
Students will become familiar with one of the famous methods of
translating of geometric/topological problems into algebraic ones as a
means of solution. They will have knowledge of the ideas oand methods of
Algebraic Topology, and will continue practice in problem solving,
conceptual thinking, logical argument and written presentation.
Methods
Lectures, examples classes, example sheets.
Assessment
Marked problem sheets, written examination.
Explanation of Pre-requisites
This module needs some knowledge of both analysis and algebra. The
analysis needed requires the student to be comfortable with discussing
reasonably straightforward topological spaces such as spheres, tori,
discs and so on, together with the idea of continuous functions between
them. This is all covered in the Abstract Analysis course MA2151, but
more familiarity with these conceps will be gained from the Topology
module MA3151 which would be a good partner with this module.
The algebra used is a combination of elementary group theory and/or
linear algebra (the student is free to choose which type of algebra they
prefer, though ideally they should be familiar with the elementary
concepts of both).
Course Description
Fact: if you have a dog which is completely covered in hair, then there
is no way of combing that hair smooth so that there is no parting or bald
spot. This is the so-called `hairy dog theorem'.
Fact: no matter how badly you make a sandwich out of two pieces of bread
and a slice of ham then it is always possible to find a plane cutting the
sandwich which bisects exactly each piece of bread and the slice of meat.
This is the so-called `ham sandwich theorem'.
Fact: if you associate to each point of the Earth's surface the two
numbers 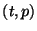 where
where 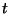 is the temperature at that point and
is the temperature at that point and 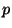 is the
air pressure there, then there is always at least one point which has the
same values of
is the
air pressure there, then there is always at least one point which has the
same values of 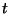 and
and 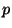 as its diametrically opposite point. This is
the `Borsuk-Ulam theorem'.
as its diametrically opposite point. This is
the `Borsuk-Ulam theorem'.
These are all very deep geometric facts about the shapes of dogs, ham
sandwiches and the Earth; they are especially deep as they are true
for any shape or size of dog, sandwich, or planet, and they are all
proved by a remarkably successful set of mathematical ideas and methods
that date from early to mid last century. These ideas, and ones like them,
constitute the subject of Algebraic Topology.
The basic idea of the subject is to find a formal way of translating
geometric problems into an appropriate algebraic language. If this is
done successfully then the geometric problem is usually reduced to a
fairly simple piece of algebra and the problem can be solved by algebraic
means. In this module we shall prove each of the facts above by
translating the underlying geometry into questions about integers, groups
or vector spaces.
Syllabus
Homology theory and homological algebra: elementary categorical concepts -
category, functor. Topological spaces, homotopy equivalent spaces,
polyhedra and the simplicial approximation theorem. Examples of standard
spaces. Simplical and singular homology groups, their functorial
properties and computation (the Eilenberg-Steenrod axioms). Relation to
the fundamental group. Application of homology theory to Brouwer's fixed
point theorem, the Ham Sandwich theorem, the hairy dog theorem and the
Borsuk Ulam theorem. Other theorems as time allows.
Reading list
Recommended:
M. A. Armstrong,
Basic Topology,
Springer.
Background:
W. S. Massey,
A Basic Course in Algebraic Topology,
Springer.
H. Sato,
Algebraic Topology: an intuitive approach,
Springer.
Resources
Problem sheets, lecture rooms, lecturer.
Module Evaluation
Module questionnaires, module review, year review.
Next: MA4111 Differential Geometry
Up: ModuleGuide03-04
Previous: MA4041 Methods in Molecular Simulation
Author: C. D. Coman, tel: +44 (0)116 252 3902
Last updated: 2004-02-21
MCS Web Maintainer
This document has been approved by the Head of Department.
© University of Leicester.
![[The University of Leicester]](http://www.le.ac.uk/corporateid/departmentresource/000066/unilogo.gif)
![[The University of Leicester]](http://www.le.ac.uk/corporateid/departmentresource/000066/unilogo.gif)
![]() where
where ![]() is the temperature at that point and
is the temperature at that point and ![]() is the
air pressure there, then there is always at least one point which has the
same values of
is the
air pressure there, then there is always at least one point which has the
same values of ![]() and
and ![]() as its diametrically opposite point. This is
the `Borsuk-Ulam theorem'.
as its diametrically opposite point. This is
the `Borsuk-Ulam theorem'.