![[The University of Leicester]](http://www.le.ac.uk/corporateid/departmentresource/000066/unilogo.gif) | Department of Mathematics |
 |
Next: MA4041 Methods in Molecular Simulation
Up: ModuleGuide03-04
Previous: MA4011 Finite Element Methods for Partial
MA4021 Wavelets and Signal Processing
| Credits: 20 |
Convenor: Dr J. Levesley |
Semester: 2 |
| Prerequisites: |
essential: MA2101 |
|
| Assessment: |
Fortnightly work, computer practicals, project: 40% |
3 hour examination: 60% |
| Lectures: |
36 |
Problem Classes: |
5 |
| Tutorials: |
none |
Private Study: |
99 |
| Labs: |
10 |
Seminars: |
none |
| Project: |
none |
Other: |
none |
| Surgeries: |
0 |
Total: |
150 |
Subject Knowledge
Aims
This module aims to show students how to use wavelets to analyse and compress signals. The tools of Fourier analysis will be developed to give a theoretical understanding of wavelet approximation. Students will also learn, via computer practicals, to actually analyse and compress digital signals.
Learning Outcomes
To learn basic harmonic analysis, to understand and apply the idea of a filter bank, to learn the mathematical and computational theory of wavelets, to be able to analyse and compress a signal using wavelets.
Methods
Lectures, computer practicals.
Assessment
Marked fortnightly work, project reports, practical diaries, examination.
Subject Skills
Aims
To provide students with report writing, oral communication and IT skills.
Learning Outcomes
Students write a project report, keep a practical log, and give an oral project presentation. They will do computer lab work.
Methods
Workshops, computer proacticals.
Assessment
Project report, project presentation, and practical diary.
Explanation of Pre-requisites
Course Description
Wavelets are very useful tools for data analysis and compression. Current research into the uses of wavelets for these and other purposes is intense. In this course you will be introduced to the mathematical theory of wavelets. One of the key tools here is harmonic analysis, which is a very useful tool in a variety of settings. You will also learn, in a practical setting, how to use wavelets to analyse and compress digital signals.
Syllabus
Filter banks. The basic space 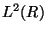 and the basic facts we need to know about it. Results about the Fourier
transform, including Parseval's identity. Brief discussion of Fourier series. Introduction to
wavelets, the Haar wavelet as an elementary model example, the two-scale equation,
multiresolution analysis, how the multiresolution analysis aids the construction of wavelets,
stable bases in
and the basic facts we need to know about it. Results about the Fourier
transform, including Parseval's identity. Brief discussion of Fourier series. Introduction to
wavelets, the Haar wavelet as an elementary model example, the two-scale equation,
multiresolution analysis, how the multiresolution analysis aids the construction of wavelets,
stable bases in 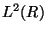 , the decomposition and reconstruction algorithms, the symbol, compactly
supported wavelets, the cascade algorithm for constructing wavelets from the two scale equation.
, the decomposition and reconstruction algorithms, the symbol, compactly
supported wavelets, the cascade algorithm for constructing wavelets from the two scale equation.
Reading list
Background:
E.W. Cheney and W.A. Light,
A Course in Approximation Theory,
Brooks Cole, 2000.
J. Prestin, in,
Tutorials on Multiresolution in
Geometric Modelling,
(Iske et. al. (eds)), Springer-Verlag, 2002.
G. Strang, in,
Wavelets, Multilevel Methods and Elliptic PDE's,
(Ainsworth et. al. (eds)), OUP, 1997.
C. K. Chui,
An Introduction to Wavelets,
Academic Press, 1992.
Resources
Computer laboratories, lecture rooms.
Module Evaluation
Module questionnaires, module review, year review.
Next: MA4041 Methods in Molecular Simulation
Up: ModuleGuide03-04
Previous: MA4011 Finite Element Methods for Partial
Author: C. D. Coman, tel: +44 (0)116 252 3902
Last updated: 2004-02-21
MCS Web Maintainer
This document has been approved by the Head of Department.
© University of Leicester.
![[The University of Leicester]](http://www.le.ac.uk/corporateid/departmentresource/000066/unilogo.gif)
![[The University of Leicester]](http://www.le.ac.uk/corporateid/departmentresource/000066/unilogo.gif)