[The University of Leicester]

Department of Mathematics



Next: MA4021 Wavelets and Signal Processing Up: ModuleGuide03-04 Previous: MA4001 Dynamical Systems

MA4011 Finite Element Methods for Partial Differential Equations

MA4011 Finite Element Methods for Partial Differential Equations

Credits: 20 Convenor: Dr. Ciprian Coman Semester: 2 (weeks 15 to 26)
Prerequisites: desirable: MA2001(=MC224), MA2121(=MC243)
Assessment: coursework: 40% 2 hour exam: 60%
Lectures: 36 Problem Classes: 10
Tutorials: none Private Study: 104
Labs: none Seminars: none
Project: none Other: none
Surgeries: none Total: 150

Subject Knowledge

Aims

The aim of this course is to introduce the basic theory of finite element methods for the numerical approximation of partial differential equations and provide a good basis for those students who wish to pursue the study of more advanced topics.

Learning Outcomes

Students should understand the mathematical framework of finite element methods. In particular they should be able to calculate weak derivatives for simple functions, formulate the weak form for a large class of elliptic partial differential equations and understand the role played by boundary conditions in obtaining the weak forms. They should be able to construct various approximations of these weak problems and be able to characterise the error bounds involved. Students should also gain some measure of familiarity with the software package MATLAB and its use in evaluating numerical algorithms.

Methods

Class sessions, computer labs and problem classes.

Assessment

The coursework will consist of regularly assigned exercise sheets, including computer assignments. A substantial individual project will be required and the student will have to present the project orally to the class and the instructor. The June examination will have 4 questions, it being (theoretically) possible to obtain full marks by answering 3 of them.

Subject Skills

Aims

To foster and develop the ability to synthesise and build upon knowledge acquired in the previous years.

The ability to apply the techniques developed in this course to a large variety of partial differential equations.

Learning Outcomes

Students will gain an appreciation of mathematical modelling and solving practical problems and in this process they will learn how to design an implement complex solutions for specific problems, and be able to present this information effectively in either written or oral form. A special emphasis will be placed on simplicity combined with depth of understanding rather than on sophistication.

Methods

Class sessions, computer lab sessions and problem classes.

Assessment

Marked problem sheets, lab reports and class tests.

Explanation of Pre-requisites

A good understanding of linear space theory and the calculus of functions of several variables. Some knowledge of MATLAB is desirable but it is not essential.

Course Description

Partial differential equations arise in the mathematical modelling of many physical, chemical and biological phenomena. Indeed, they play a crucial role in many diverse subject areas, such as fluid dynamics, electromagnetism, materials science, astrophysics and financial modelling, for example. Typically, the equations under consideration are so complicated that their solution may not be determined by purely analytical techniques; instead one has to resort to computing numerical approximations to the unknown analytical solution. This course is devoted to a particular class of numerical techniques for determining the approximate solution of partial differential equations: finite element methods. Here, we will provide an introduction to their mathematical theory, with special emphasis on theoretical and practical issues such as accuracy, reliability and implementation.

Syllabus

Review of the linear space theory. Hilbert space theory (subspaces and projections). Riesz representation theorem; Lax Milgram lemma.

Basic facts about function spaces; 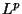$L^p$-spaces and Sobolev spaces. The theory of weak solutions to elliptic boundary value problems.

Finite element methods for elliptic partial differential equations; Galerkin orthogonality; Cèa's lemma; piecewise polynomial approximation in Sobolev spaces; optimal error bounds in the energy norm; Aubin-Nitsche duality argument; variational crimes.

A posteriori error analysis by duality.

Computer implementation of FEM algorithms for simple problems.

Reading list

Recommended:

K. Eriksson, D. Estep, P. Hansbo and C. Johnson, Computational Partial Differential Equations, Cambridge University Press, 1996.

C. Johnson, Numerical Solution of Partial Differential Equations by the Finite Element Method, Cambridge University Press, 1990.

W. Cheney, D. Kincaid, Numerical Mathematics and Computing (fifth edition), Brooks Cole, 2003.

P.G. Ciarlet, The Finite Element Method for Elliptic Problems, North-Holland, 1978.

S. Brenner and R. Scott, The Mathematical Theory of Finite Element Methods, Springer-Verlag, 1994.

Resources

Problem sheets, handouts, computer labs and lecture rooms.

Module Evaluation

module questionnaires, module review, year review.

Next: MA4021 Wavelets and Signal Processing Up: ModuleGuide03-04 Previous: MA4001 Dynamical Systems

[University Home] [MCS Home] [University Index A-Z] [University Search] [University Help]

Author: C. D. Coman, tel: +44 (0)116 252 3902
Last updated: 2004-02-21
MCS Web Maintainer
This document has been approved by the Head of Department.
© University of Leicester.