[The University of Leicester]

Department of Mathematics



Next: MA3201 Generalized Linear Models Up: ModuleGuide03-04 Previous: MA3131 Group Theory

MA3151 Topology

MA3151 Topology

Credits: 20 Convenor: Dr. F. Neumann Semester: 1 (weeks 2 to 12)
Prerequisites: essential: MA1101, MA1102, MA2151
Assessment: Coursework: 10% Three hour examination in January: 90%
Lectures: 36 Problem Classes: 10
Tutorials: none Private Study: 104
Labs: none Seminars: none
Project: none Other: none
Surgeries: none Total: 150

Subject Knowledge

Aims

This module aims to explore geometric objects such as knots, surfaces or general topological spaces and how elementary algebra and analysis can provide a rigorous language for discussing their properties.

Learning Outcomes

Students should know the definitions of and understand the key concepts introduced in this module.

Students should be able to understand, reproduce and apply the main results and proofs in this module.

Students should be able to solve some routine topological problems.

Methods

Class sessions and supervision groups.

Assessment

Marked problem sheets, written examination.

Subject Skills

Aims

To provide students with problem solving skills and develop written communication skills.

Learning Outcomes

Students will be able to use the techniques taught within the module to solve problems, to present arguments and solutions in a coherent and logical form and to apply taught principles and concepts to new situations.

Methods

Class sessions, supervison groups.

Assessment

Marked problem sheets, written examination.

Explanation of Pre-requisites

This module will draw on some basic ideas from both algebra and analysis. In algebra knowledge will be assumed of basic number systems and of the idea of a group and associated ideas. In analysis the central topics drawn on are the ideas of topological spaces, of closed or compact subsets of 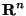${\bf R}^n$ and continuous functions.

Course Description

Many geometric ideas turn out not really to depend on size or distance - thus for example, a Möbius band has only one side however large or small it is; a knotted loop of string remains knotted however much the string is pulled and twisted about, and the surface of a donut or bicycle inner-tube cannot be deformed into the surface of a ball without cutting and pasting parts of it together. All these observations are about underlying properties of the objects and the study of such ideas is called topology.

This module introduces the main ideas, in particular the central concepts of homotopy and the fundamental group.

This module represents a branch of mathematics which brings together many of the basic ideas of algebra and analysis met before in the course as well as linking many of the later topics. Ideas in the module will particularly complement the 3rd year module MA3121 Complex Analysis and the 4th year modules MA4111 Differential Geometry and MA4101 Algebraic Topology which run in alternate years.

Syllabus

Topological spaces, continuous maps, examples, group actions, homotopy, the fundamental group and its properties, calculations of fundamental groups, covering spaces, applications such as knot theory or classification of surfaces, as time allows.

Reading list

Recommended:

Recommended:

M. A. Armstrong, Basic Topology, Springer.

G.E. Bredon, Topology and Geometry, Springer.

W. Fulton, Algebraic Topology: A first course, Springer.

L. C. Kinsey, Topology of Surfaces, Springer.

J.R. Munkres, Topology: a first course, Prentice-Hall, Inc..

A. Hatcher, Algebraic Topology, Cambridge.

Background:

K. Jähnich, Topology, Springer.

H. Sato, Algebraic Topology: an intuitive approach, Springer.

Resources

Problem sheets, additional handouts, lecture rooms.

Module Evaluation

Module questionnaires, module review, year review.

Next: MA3201 Generalized Linear Models Up: ModuleGuide03-04 Previous: MA3131 Group Theory

[University Home] [MCS Home] [University Index A-Z] [University Search] [University Help]

Author: C. D. Coman, tel: +44 (0)116 252 3902
Last updated: 2004-02-21
MCS Web Maintainer
This document has been approved by the Head of Department.
© University of Leicester.