[The University of Leicester]

Department of Mathematics



Next: MA2101 Real Analysis Up: ModuleGuide03-04 Previous: MA2071 Scientific Computing

MA2081 Methods of Applied Mathematics II

MA2081 Methods of Applied Mathematics II

Credits: 20 Convenor: Dr. J. Levesley Semester: 2 (weeks 13 to 24)
Prerequisites: essential: MA1001, MA1002, MA1051
Assessment: Weekly exercises and computer practical: 40% 3 hour exam: 60%
Lectures: 33 Problem Classes: 10
Tutorials: none Private Study: 85
Labs: 11 Seminars: none
Project: none Other: none
Surgeries: 11 Total: 150

Subject Knowledge

Aims

This module aims to introduce the student to fundamental methods in applied mathematics, to give the student experience and in using the computer to solve mathematical problems. The course also aims to provide a mathematical introduction to the mechanics of inviscid fluids, and to apply the theory to wave phenomena. Waves in other media may also be considered.

Learning Outcomes

To know scalar, vector and triple products and their use in the description of lines and planes, the summation convention including the Kronecker delta 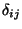$\delta_{ij}$ and the alternating tensor 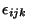$\epsilon_{ijk}$, the definitions of, and to be able to use, the vector differential operators grad, div and curl, and the Laplacian. To be able to work with line, surface and volume integrals, state and use in simple cases Green's theorem in the plane, the divergence theorem and Stokes' theorem.

To know how to describe fluid flow, to understand the role of contact forces, and to learn how to use the concept of pressure, to be able to use the basic equations of inviscid fluid dynamics in a variety of simple situations, to understand the basic concepts of wave motion - wave equation, frequency, wavelength.

Methods

Lectures, computer classes, problem classes.

Assessment

Marked problem sheets, computer practical portfolio, examination.

Subject Skills

Aims

To provide students with computing skills and develop written communication skills and problem solving skills.

Learning Outcomes

Students will have used a computer to solve some simple mathematical problems, and recorded their findings in a portfolio. Students will have improved their ability ot solve problems both using pencil and paper and a computer.

Methods

Lectures, computer classes, problem classes.

Assessment

Marked problem sheets, marked computer practical portfolio.

Explanation of Pre-requisites

The work on vectors, curves, partial differentiation and multiple integrals, which was covered in MA1001, will form a basis for this module. A general mathematical knowledge from other modules is also required.

Course Description

This module will extend the vector algebra of the first year to the calculus of three dimensional vectors. This is an essential module for those wishing to take certain later modules in Applied Mathematics, for example Fluids and Waves, General Relativity, Electromagnetic Theory etc. The course also develops the ideas of mechanics to a continuous medium using the mathematical tools learnt in the earleir part of the module.

Syllabus

Introduction to vector algebra.

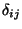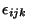Introduction of suffix notation and the summation convention including $\delta_{ij}$ and $\epsilon_{ijk}$.

The vector differential operators grad, div and curl.

Line, surface and volume integrals with particular application to the divergence theorem and Stokes' theorem.

Fluids, density, velocity field, conservation of mass. Pressure, material derivative, Euler's equation. Hydrostatics, liquids and gases, atmospheric equilibrium. Steady flow, streamlines, Bernoulli's equation. Streams of constant breadth. Vorticity, irrotational motion. Compressible flow, sound waves. Other examples of wave motion.

Reading list

Recommended:

C. H. Edwards and D. E. Penney, Calculus, Pearson Education, 2002.

J.E. Marsden and A.J. Tromba, Vector Calculus, W H Freeman & Co.; ISBN: 0716724324.

Background:

D.J.Acheson, Elementary Fluid Dynamics, Oxford. This book contains considerably more material than is covered in this module, but chapters 1 and 3 give a good coverage of most of the topics required..

Background:

M. R. Spiegel, Vector Analysis, Schaum Outline Series.

H. P. Hsu, Applied Vector Calculus, Harcourt Brace Jovanovich College Outline Series.

E. A. Maxwell, Coordinate Geometry with Vectors and Tensors, CUP? Probably out of print..

J. Gilbert, Guide to Mathematical Methods, MacMillan.

P.C. Matthews, Vector Calculus, Springer
There are in addition a number of Vector Analysis texts located at 515.63 in the Library.

Resources

Problem sheets, computer rooms, lecture rooms.

Module Evaluation

Module questionnaires, module review, year review.

Next: MA2101 Real Analysis Up: ModuleGuide03-04 Previous: MA2071 Scientific Computing

[University Home] [MCS Home] [University Index A-Z] [University Search] [University Help]

Author: C. D. Coman, tel: +44 (0)116 252 3902
Last updated: 2004-02-21
MCS Web Maintainer
This document has been approved by the Head of Department.
© University of Leicester.