![[The University of Leicester]](http://www.le.ac.uk/corporateid/departmentresource/000066/unilogo.gif) | Department of Mathematics |
 |
Next: MA2081 Methods of Applied Mathematics II
Up: ModuleGuide03-04
Previous: MA2061 Lagrangian and Hamiltonian Dynamics
MA2071 Scientific Computing
| Credits: 10 |
Convenor: Dr Paul Houston |
Semester: 2 |
| Prerequisites: |
|
desirable: MA1151(=MC146), MA1152(=MC147), MA2101(=MC248) |
| Assessment: |
Coursework: 50% |
One and a half hour exam: 50% |
| Lectures: |
18 |
Problem Classes: |
5 |
| Tutorials: |
none |
Private Study: |
47 |
| Labs: |
5 |
Seminars: |
none |
| Project: |
none |
Other: |
none |
| Surgeries: |
none |
Total: |
75 |
Subject Knowledge
Aims
By the end of this module the student should:
- appreciate the interplay among
the elements of modern scientific computing, including
modelling, simulation, and error analysis;
- be familiar with a few of the basic algorithms for solving linear
systems, nonlinear equations, and ordinary differential equations;
- gain some measure of familiarity with the software package MATLAB
and
its use in evaluating numerical algorithms.
Learning Outcomes
Students should know the definitions of and understand the key mathematical
concepts and their relationship to the general problems which motivate their
consideration in each of the topics of this module.
Methods
Class sessions and laboratories together with some handouts.
Assessment
Marked problem sheets.
Subject Skills
Aims
This course will impart a basic understanding of some of the key methods of
scientific computing as well as an introduction to software tools such
as MATLAB.
These skills are important in all areas of modern applied
science and engineering and are also widely used in industry.
Learning Outcomes
Students will be able to
use the techniques taught within the module to solve problems, and be able
to present arguments and solutions in a coherent and logical form.
Methods
Class sessions, laboratories.
Assessment
Marked problem sheets, projects.
Explanation of Pre-requisites
Students have learned in MA1152 about the structure of
linear systems of
algebraic equations and something of methods for solving such problems.
Here they
will see how these techniques can be applied to solve problems arising
in
engineering and science applications. The concept of an eigenvalue
(also from MA1152)
will be used in the analysis of the Jacobi and Gauss-Siedel iterations.
Ideas and
techniques from MA1151 and MA2101 are used in error analysis for all types
of problems.
Course Description
This course introduces some of the methods and ideas used in applied
numerical modelling, such as one typically encounters in chemistry,
physics and engineering problem-solving. The problem is usually to
determine,
for given input data, an approximate solution to an equation or system
of equations
that is accurate to some desired error tolerance. The challenge is to
find ways to
do this efficiently and
to analyze the effects of various types of errors on the quality of the
approximation.
The dimension of systems that arise in real-world applications can be
quite large,
and it is therefore essential to build algorithms whose complexity
scales reasonably with the
problem size. Sometimes a particular structure is present in the
problem formulation
which can improve the numerical treatment. For example, it is often
possible to solve
symmetric matrices more reliably and accurately than nonsymmetric ones
of equivalent dimension.
Many of the most important numerical tasks have to do with approximating
the solutions of differential equations. For the purposes of
illustrating the
process, we restrict attention to a few elementary
(scalar) ordinary differential equations, and a few popular schemes for
their numerical approximation.
The convergence of a given method is dependent on two important
properties:
the magnitude of the perturbations or local error introduced at
each stage of the calculation, and
stability which relates to the rate of growth of perturbations
through the
many steps of a long computational process. We are often faced with
the task of comparing
two methods, in which case the order of accuracy of the method
becomes important.
Besides introducing some of the theoretical issues of numerical
analysis, this course
will give students a taste of modern scientific computing software
tools, especially the
MATLAB package which facilitates interactive evaluation of numerical
methods and graphical
visualization of the results of simulation.
As part of the course, students will complete a series of
computer projects using
MATLAB.
Syllabus
- 1. Models and Methods
-
- Mathematical Models
- Ordinary Differential Equations
- Discretization
- Algorithms
- Types of Error and norms.
- 2. Two-point BVPs and linear systems
-
- Simple models, e.g.
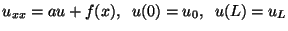
- Finite difference discretization and linear systems
- LU and Cholesky factorization
- Jacobi and Gauss-Siedel iterations
- 3. Nonlinear Equations and Iterations
-
- Models and implicit functions, Root-finding and Kepler's
equation.
- Fixed point iterations
- linear vs. superlinear convergence
- Newton's method and 2nd order convergence
Reading list
Recommended:
D. Kincaid and W. Cheney,
Numerical Analysis,
Brooks/Cole.
R. L. Burden and J. Douglas Faires,
Numerical Analysis,
PWS-Kent.
Resources
Problem sheets and laboratories.
Module Evaluation
Module questionnaires, module review, year review.
Next: MA2081 Methods of Applied Mathematics II
Up: ModuleGuide03-04
Previous: MA2061 Lagrangian and Hamiltonian Dynamics
Author: C. D. Coman, tel: +44 (0)116 252 3902
Last updated: 2004-02-21
MCS Web Maintainer
This document has been approved by the Head of Department.
© University of Leicester.
![[The University of Leicester]](http://www.le.ac.uk/corporateid/departmentresource/000066/unilogo.gif)
![[The University of Leicester]](http://www.le.ac.uk/corporateid/departmentresource/000066/unilogo.gif)