Next: MC360 Stochastic Modelling
Up: Year 3
Previous: MC347 Coding Theory
MC349 Complex Analysis
| Credits: 20 |
Convenor: Prof. G. Robinson |
Semester: 2 |
| Prerequisites: |
essential: MC146, MC240,MC248 |
|
| Assessment: |
Regular coursework: 20% |
Three hour exam: 80% |
| Lectures: |
36 |
Classes: |
12 |
| Tutorials: |
12 |
Private Study: |
102 |
| Labs: |
none |
Seminars: |
none |
| Project: |
none |
Other: |
none |
| Total: |
150 |
|
|
Explanation of Pre-requisites
The student will be assumed to be familiar with the
general notion of continuity of a real function as
well as other basic concepts from Real Analysis.
It would be useful to be familiar with differentiability
of real functions, power series and integration.
Course Description
In many ways, the subject of Complex Analysis is
aesthetically more pleasing than Real Analysis,
several of the results being ``cleaner'' than their
real counterparts. In this course, we begin with
the study of analogues
for complex functions of familiar properties of
real functions, though differences in the two theories
qucikly emerge. The theory of complex integration
is developed, culminating in a number of strikingly
beautiful applications. Towards the end of the course,
the results from complex integration theory are used
to evaluate certain real integrals and evaluate
the sums of certain real infinite series.
Aims
To help the student to develop an appreciation of the rigorous development
of this beautiful subject, and an understanding of the fundamental
results of the subject.
Objectives
To enable the student to :
Determine whether a function is complex differentiable.
Understand how to determine the radius of convergence
of a power series.
Define and evaluate path integrals.
Understand, prove and use Cauchy's integral theorem
and Cauchy's integral formula.
Understand Taylor's theorem and appreciate that a function
which is differentiable in a neighbourhood of a point
has a Taylor series expansion about that point.
Understand Laurent's theorem and appreciate that a function
which is differentiable in a punctured neighbourhood of a point
has a Laurent expansion about that point.
Determine whether a function has a singularity at a given point,
and the nature and order ( if applicable) of the singularity.
Calculate residues and use the residue theorem to evaluate
integrals around simple closed paths.
Use the residue theorem to evaluate certain real integrals,
to evaluate the sum of certain real series and to assist in
certain partial fraction decompositions.
Transferable Skills
This course should assist the student in developing skills
of rigorous and precise Mathematical writing and expression.
It should also provide useful techniques and results for
other level three and level four courses.
Syllabus
Review of the complex number field. Cauchy-Riemann equations.
Complex power series and some functions defined by them.
Radius of converegence, term-by-term differentiability of functions
defined by a power series with positive radius of convergence.
Path integrals. Simple closed paths. Star-shaped domains.
Cauchy's integral theorem. Cauchy's integral formula.
Taylor's theorem. Entire functions. Liouville's theorem and its application
to the fundamental theorem of algebra. Laurent series.
Singularities, poles, residues. The order of a function at a singularity.
Orders of poles. The residue theorem and some techniques for
calculating residues.
Rouche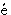
's theorem, the principal of the argument.
Use of the residue theorem to evaluate real integrals and
to evaluate sums of certain real series. Partial fractions.
Reading list
Essential:
Background:
GJO Jameson,
A First Course on Complex Functions,
out of print.
Recommended:
I. Stewart and D. Tall,
Complex Analyis,
Cambridge University Press.
H.A. Priestley,
Introduction to Complex Analysis,
Oxford University Press.
Details of Assessment
The coursework will consist of regularly assigned
exercise sheets. The June examination will have 6 questions,
it being (theoretically) possible to obtain full marks by answering 4 of
them.
Next: MC360 Stochastic Modelling
Up: Year 3
Previous: MC347 Coding Theory
Roy L. Crole
10/22/1998