


Next: MC480 Mathematics Project
Up: Year 4
Previous: MC449 Galois Theory
MC460 Statistical Inference
| Credits: 20 |
Convenor: Mr. B. English |
Semester: 2 |
| Prerequisites: |
essential: MC160, MC161, MC260 |
desirable: MC261 |
| Assessment: |
Coursework: 10% |
Three hour exam: 90% |
| Lectures: |
36 |
Classes: |
none |
| Tutorials: |
12 |
Private Study: |
102 |
| Labs: |
none |
Seminars: |
none |
| Project: |
none |
Other: |
none |
| Total: |
150 |
|
|
Explanation of Pre-requisites
Modules MC160 and MC260 provide the core probability and distribution theory
for this course, while MC161 provides necessary introductory material on the
likelihood function, hypothesis testing and confidence intervals. The module
MC261 reinforces and extends material from these earlier modules
and is therefore,
given the importance of this material, a desirable prerequisite. Further,
methods covered informally in MC261 provide motivation for a more formal analysis
in this module.
Course Description
This module discusses general principles which may be used to derive
classical procedures introduced informally in earlier modules.
For example, apart from their intuitive reasonableness, can the t-test and
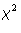 -goodness-of-fit test, be given more formal foundations within a more
general theory of hypothesis testing?
-goodness-of-fit test, be given more formal foundations within a more
general theory of hypothesis testing?
In a more formal appraisal of estimation, we consider the problem of finding a
`best' estimator, how the best unbiased
estimator (if it exists) may be found, and question whether such estimators are
desirable.
The theoretical support for the method of maximum likelihood estimation is
considered, and some of its limitations are identified.
Detailed consideration is given
to inferences based on the
large-sample properties of the maximum likelihood estimator, and their
asymptotic equivalents.
Such methods play a key role in
much modern applied statistical analysis.
We also discuss a number of standard inferential topics from a Bayesian
standpoint; an increasingly important
approach over the last two decades, and consider some aspects
of the debate between adherents of the Bayesian and Frequentist
approaches to inference.
Aims
To discuss and illustrate some of the general principles
which may be exploited to derive various
classical statistical procedures introduced
informally in earlier modules. To expose students to some of the
elegant results and more thorny and fascinating questions of statistical
inference, to encourage further study. To this end,
we discuss some aspects of the debate between adherents of the Bayesian
and Frequentist approaches to inference.
To provide a solid grounding for inferences based on the
large-sample properties of the maximum likelihood estimator, and their
asymptotic equivalents. Such methods play a key role in
much modern applied statistical analysis.
Objectives
On completion of this module, students should:
- be able to write down a likelihood function for various types of data,
obtain the maximum likelihood estimator and provide sufficient statistics;
- know the definition of sufficient statistic (both classical and Bayesian),
minimal sufficient statistic, the Factorisation Theorem and its application;
- in the context of point estimation, understand what is meant by
the terms; loss function, admissible and inadmissible, and unbiased.
- know the Cramér-Rao lower-bound for the variance of an unbiased
estimator; conditions for its validity and for its attainment, and be able to
exploit it in appropriate situations;
- know and understand the implications of the Rao-Blackwell and
Lehmann-Scheffé Theorems and be able to apply them;
- know what is meant by, and be aware of the pros and cons of unbiased,
maximum likelihood, min-max and Bayes' estimators;
- be able to state the asymptotic distribution of the maximum likelihood
estimator (for one or more parameters), under appropriate regularity conditions
(to be understood), and be able to apply these, and asymptotic equivalents
to constructing approximate tests and confidence intervals;
- be aware of how prior distributions may be elicited, and how
posterior distributions and Bayes' estimates are computed;
- know the Neyman-Pearson Lemma and associated technical terms, and be able
to apply it in simple cases;
- understand what is meant by a uniformly most powerful test and an unbiased
test, and be able to find such tests in appropriate situations;
- know what is meant by a score statistic, its motivation, its application
and asymptotic distribution;
- know how to construct a likelihood-ratio test; its motivation and
application; Wilks theorem;
- understand what is meant by a classical confidence interval and its
relationship to significance tests; understand the interpretation of a Bayesian
credible interval and how this differs from the classical confidence interval;
- be able to apply the Fieller-Creasy method to appropriate problems, and
explain the concept of a recognisable subset;
- know what is meant by an ancillary statistic and understand its
significance for frequentist and Bayesian inference.
Transferable Skills
- A reasonable knowledge of some of the basic ideas of modern statistical
inference should provide a good foundation for postgraduate work in many areas.
- A knowledge of the basic asymptotic theory of the maximum likelihood
estimator and related statistics is an essential prerequisite for many of the
more sophisticated techniques of applied statistical analysis,
including applications of the generalised linear model.
- The ability to formalise and analyse a problem, and present a logically
argued solution.
Syllabus
A review and extensions of some distribution theory; bivariate distributions for
variables of mixed types; the multinomial distribution and its basic properties;
order statistics. Chebyshev's inequality, the Weak and Strong Laws of large
numbers.
The likelihood function, the weak and strong likelihood principles.
Competing approaches to inference; the frequentist and Bayesian approach. The
specification of prior distributions and computation of posterior distributions;
an example of Bayesian inference; other approaches.
Sufficient statistics; frequentist and Bayesian definitions; the factorisation
theorem. Point estimation; loss functions, risk functions, admissibility,
unbiasedness and consistency. Unbiased estimates; the Cramér-Rao inequality,
the Rao-Blackwell and Lehmann-Scheffé Theorems. The pros and cons of unbiased
estimators. The maximum likelihood estimator, its asymptotic
distribution (for one or more parameters, under suitable regularity conditions);
asymptotic equivalents, and use for
providing approximate tests and confidence intervals. The pros and cons of
maximum likelihood estimation.
Bayesian and mini-max estimators, and their calculation.
Hypothesis testing; the Neyman-Pearson Lemma, uniformly most powerful
tests, unbiased tests. Tests based on the large sample properties of the
maximum likelihood estimate, likelihood ratio test (Wilks' Theorem),
and score statistic. Fisher's approach.
The Bayesian approach to significance tests and Lindley's paradox.
Confidence intervals and regions, their relationship to hypothesis testing; the
Fieller-Creasy method, and recognisable subsets. Bayesian credible intervals.
Ancillary statistics, the ancillarity principle, and conditional likelihoods.
Reading list
Background:
V. Barnett,
Comparative Statistical Inference,
J. Wiley, 1973.
D. R. Cox and D. V. Hinkley,
Theoretical Statistics,
Chapman and Hall, 1974.
M. H. DeGroot,
Probability and Statistics, 2nd edition,
Addison-Wesley, 1986.
S. D. Silvey,
Statistical Inference,
Chapman and Hall, 1975.



Next: MC480 Mathematics Project
Up: Year 4
Previous: MC449 Galois Theory
Roy L. Crole
10/22/1998