


Next: MC440 Commutative Algebra
Up: Year 4
Previous: MC430 Approximation Theory
MC433 Partial differential equations: Solitons
| Credits: 20 |
Convenor: Dr M. Ainsworth |
Semester: 2 |
| Prerequisites: |
|
desirable: MC224 |
| Assessment: |
Coursework: 10% |
Three hour exam: 90% |
| Lectures: |
36 |
Classes: |
none |
| Tutorials: |
12 |
Private Study: |
102 |
| Labs: |
none |
Seminars: |
none |
| Project: |
none |
Other: |
none |
| Total: |
150 |
|
|
Course Description
Solitons are a class of nonlinear waves which keep their size and form in
isolation. However, when they meet one another they lose, but soon regain,
their size and form, almost as if they were fundamental particles like
electrons and neutrons. Solitons have a host of important applications in
many branches of physics (e.g. nonlinear optical fibres, polymer mechanics,
water waves, fundamental particles), and are solutions of certain nonlinear
partial differential equations.
The core of the course will be the theory of the inverse scattering transform,
a major achievement of twentieth-century mathematics, which explains why
solitons regain their size and form after interacting strongly with one
another. This theory will be motivated by several examples of nonlinear waves,
introduced by a review of linear scattering theory, and subsequently applied
to examples of soliton equations, such as the Korteweg-deVries equation
and the sine-Gordon equation.
Aims
The course aims to introduce ideas of nonlinear waves in general, and solitons
in particular, with explanation of the inverse scattering transform and
indication of the many applications of the theory in science.
Objectives
At the end of the course the students should appreciate the importance of
solitons and understand the seemingly miraculous property of solitons passing
through one another and behaving as if they were particles.
Syllabus
Introduction to linear waves, dispersion, nonlinear waves, method of
characteristics, shock waves, the history of the discovery of solitons and
the Korteweg-de Vries equation.
Waves of Permanent Form. Cnoidal and solitary waves. Other examples.
Scattering and Inverse Scattering Problems. Bound states and discrete
spectrium; scattering and continuous spectrum.
Inverse Scattering Transform for the KdV Equation. Flow diagram of method.
The method. Reflectionless potentials. Examples.
Conservation Laws.
Lax Methods. Lax pairs. Other methods. Examples.
Sine-Gordon Equation. Introduction. Waves of permanent
form. Breathers. Inverse Scattering.
Reading list
Essential:
P. G. Drazin & R. S. Johnson,
Solitons - An Introduction,
Cambridge University Press, 1992. 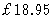 .
.
Recommended:
A.C. Newell,
Solitons in mathematics and physics,
SIAM Philadelphia, 1985.
R.K. Dodd, J.C. Eilbeck, J.C. Gibbon & H.C. Morris,
Solitons and non-linear wave equations,
Academic Press, London, 1982.
Background:
G. L. Lamb,
Elements of Soliton Theory,
Wiley, 1980.
G. B. Whitham,
Linear and Nonlinear Waves,
Wiley, 1974.



Next: MC440 Commutative Algebra
Up: Year 4
Previous: MC430 Approximation Theory
Roy L. Crole
10/22/1998
![]() .
.