Next: Year 3
Up: Year 2
Previous: MC264 Linear Statistical Models
MC265 Introductory Statistics
| Credits: 10 |
Convenor: Mr. B. English |
Semester: 1 (weeks 1 to 6) |
| Prerequisites: |
essential: MC160 |
|
| Assessment: |
Coursework: 20% |
One and a half hour examination: 80% |
| Lectures: |
18 |
Classes: |
5 |
| Tutorials: |
none |
Private Study: |
52 |
| Labs: |
none |
Seminars: |
none |
| Project: |
none |
Other: |
none |
| Total: |
75 |
|
|
Explanation of Pre-requisites
The module MC160 provides the basic probabilistic ideas for
an introductory course in statistical methods.
Course Description
Statistics and statistical statements are almost unavoidable in many areas
modern science.
This course introduces some of the central ideas of modern statistical
reasoning, and presents a
number of the more basic procedures of elementary applied
statistics.
Aims
To introduce the main concepts of statistical
inference; point and interval estimation, and hypothesis testing.
The likelihood function and maximum likelihood estimate, key concepts in much
modern statistical analysis, are also introduced.
Objectives
On completion of this module, students should:
- know what is meant by an estimate, an estimator, and a
sampling distribution;
- understand what is meant by an unbiased estimator;
- know the mean and variance of the sampling distribution of the sample
mean;
- know how to write down a likelihood function and find a maximum likelihood
estimate for simple models;
- have an informal understanding of the process of hypothesis testing and
the meaning of P-values;
- know what is meant by a confidence interval and the relationship
between confidence intervals and hypothesis tests;
- be able to apply a number of simple standard statistical procedures,
recognise when these procedures are appropriate, and interpret the results of
these procedures.
Transferable Skills
- An understanding of some basic statistical concepts
including point and interval estimation, and hypothesis testing.
- The ability to implement and interpret the results of some simple
statistical procedures, and recognise when such procedures are appropriate.
Syllabus
Basic graphical methods and descriptive statistics.
Different approaches to inference.
Point estimation; mean squared errors, variance and bias. Estimates, estimators
and sampling distributions. Standard unbiased estimators of a population mean
and variance. Likelihood and the maximum likelihood estimator.
Hypothesis testing and confidence intervals. Inferences for the normal, binomial
and Poisson distributions. Comparing two populations. Small sample results for
normal populations; the t-test. Paired and unpaired samples, the F and
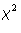distributions.
Simple examples of the 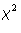goodness-of-fit test.
Reading list
Recommended:
M. H. DeGroot,
Probability and Statistics, 2nd edition,
Addison-Wesley, 1986.
J. E. Freund and R. E. Walpole,
Mathematical Statistics, 3rd edition,
Prentice-Hall.
W. Mendenhall, R. L. Scheaffer and D. D. Wackerly,
Mathematical Statistics with Applications, 4th edition,
Duxbury Press, 1990.
Details of Assessment
The final assessment of this module will consist of 20% coursework
and 80% from a one and a half hour examination during the January exam
period. The 20% coursework contribution will be determined by students'
solutions to coursework problems. The examination paper will contain
4 questions with full marks on the paper obtainable from 3 complete answers.
Next: Year 3
Up: Year 2
Previous: MC264 Linear Statistical Models
S. J. Ambler
11/20/1999