Next: MC262 Linear Regression Models
Up: Year 2
Previous: MC249 Rings and modules
MC260 Mathematical Statistics
| Credits: 10 |
Convenor: Mr. B. English |
Semester: 1 (weeks 7 to 12) |
| Prerequisites: |
essential: MC160 |
desirable: MC265 |
| Assessment: |
Coursework: 20% |
One and a half hour examination: 80% |
| Lectures: |
18 |
Classes: |
5 |
| Tutorials: |
none |
Private Study: |
47 |
| Labs: |
5 |
Seminars: |
none |
| Project: |
none |
Other: |
none |
| Total: |
75 |
|
|
Explanation of Pre-requisites
The module MC160 provides the basic introduction to
probability and univariate random variables upon which this module
builds. A number of distributional results,
derived formally in this module, were stated and exploited in module MC265;
this therefore, provides a practical motivation for the theoretical development
presented in this module.
Course Description
In this module we introduce the basic concepts and techniques
required for study of the joint behaviour of random variables, and
functions of random variables. These techniques are exploited to derive some
the classical distributions of mathematical statistics, including the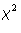 
,t and F distributions. We also introduce the multivariate normal
distribution (an extension of the normal distribution to several random
variables), and derive some of its basic properties. We also provide a proof of
the Central Limit Theorem. The course also provides an introduction to the
Minitab package.
Aims
To introduce some of the basic concepts, and provide a
practical grounding in techniques
required for study of the joint behaviour of random variables, and
functions of random variables. To reinforce the student's knowledge of the
relationships between the basic distributions of mathematical statistics.
Objectives
On completion of this course, students should:
- be able to compute moment generating functions and probability
generating functions and exploit these to obtain moments and the
distributions of functions of random variables, and limiting distributions;
- know what is meant by a joint probability distribution or probability
density function, a marginal distribution and a conditional distribution;
- be able to construct a joint distribution in simple examples;
- know how to obtain marginal and conditional distributions from
joint distributions;
- be able to find expectations, variances, covariances, correlations,
regressions and conditional variances from joint distributions, and understand
their significance;
- know how to determine the distribution (or joint distribution) of
functions of one or more random variables using appropriate techniques, which
include the use of moment generating functions, probability generating
functions, the distribution function, and Integral Transformation Theorem.
Transferable Skills
- Maintain and extend students basic calculus skills including series
expansion and summation, and univariate and bivariate integration.
- Provide further essential probabilistic concepts and mathematical
techniques for later modules in probability and statistics.
Syllabus
Review of univariate distributions. Moment generating functions; theorem on
uniqueness of the corresponding distribution; the moment generating function and
convergence in distribution. Application: a proof of the DeMoivre-Laplace Limit
Theorem. Probability generating functions. The gamma and beta functions.
Multivariate random variables (mainly restricted to bivariate random variables).
Joint distributions; marginal and conditional distributions; independence.
Expectations, conditional expectations and regression; covariance and the
coefficient of correlation.
Theorems: Unconditional means and variance from conditional means and variances;
linear regression and the coefficient of correlation.
Introduction to bivariate integrals; bivariate continuous random variables,
joint probability density functions; marginal and conditional distributions. Joint
moment and probability generating functions. The bivariate normal distribution
and its basic properties.
Functions of random variables. Functions of a single random variable. Use of the
moment and probability generating functions to find the distribution
of functions of random variables; examples including the derivation of the
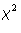distribution, the sum of independent Poisson variables, and the Central
Limit Theorem. Functions of
continuous random variables via the distribution function; the distribution of
sums, ratios and products of random variables; examples include the
derivation of the F distribution.
The distribution of functions of random variables via the Integral Transformation
Theorem; examples to include the distribution of linear combinations of
independent normal random variables.
Reading list
Recommended:
M. H. DeGroot,
Probability and Statistics, 2nd edition,
Addison-Wesley, 1986.
J. E. Freund and R. E. Walpole,
Mathematical Statistics, 3rd edition,
Prentice-Hall.
W. Mendenhall, R. L. Scheaffer and D. D. Wackerly,
Mathematical Statistics with Applications, 4th edition,
Duxbury Press, 1990.
Details of Assessment
The final assessment of this module will consist of 20% coursework
and 80% from a one and a half hour examination during the January exam
period. The 20% coursework contribution will be determined by students'
solutions to coursework problems. The examination paper will contain
4 questions with full marks on the paper obtainable from 3 complete answers.
Next: MC262 Linear Regression Models
Up: Year 2
Previous: MC249 Rings and modules
S. J. Ambler
11/20/1999