| Credits: 20 | Convenor: Dr. N. Ghani | Semester: 1 |
| Prerequisites: | essential: MC103, MC104 | desirable: MC111 |
| Assessment: | Continual assessment: 40% | Three hour exam in January: 60% |
| Lectures: | 36 | Classes: | none |
| Tutorials: | 12 | Private Study: | 78 |
| Labs: | 24 | Seminars: | none |
| Project: | none | Other: | none |
| Total: | 150 |
A grounding in the basic mathematical concepts of sets, functions and relations, and graphs is required, but detailed knowledge of other areas of elementary discrete mathematics and logic is not essential.
For many applications, the chief concern should be to produce a language which is concise and elegant. It should be expressive enough for a programmer to work productively and efficiently but simple enough to minimize the chance of making serious errors. Rapid development requires the programmer to be able to write algorithms and data structures at a high level without worrying about the details of their machine-level implementation. These are some of the criteria which have led researchers to develop the functional programming language Haskell.
The flavour of programming in Haskell is very different from that in an imperative language. Much of the irrelevant detail has been swept away. For example, there are at least three different uses for a variable in Pascal: as a storage location, as parameter in a function or procedure, as a temporary name for another variable (a `var parameter'). There is only one use for a variable in Haskell: it stands for a quantity that you don't yet know, as is standard in mathematical practice. The constructs in Pascal include expressions, commands, functions and procedures (the last two are confused in C); whereas in Haskell there are only expressions and functions. The meaning of a program in Pascal or C is understood by the effect it has on the `state' of the machine as it runs. Haskell does away with the idea of `state' -- the meaning of a program is understood by the values it computes.
On the other hand, Haskell is a very expressive language. The type system allows functions to be written polymorphically so that the same code can be re-used on data of different types, e.g. the same length function works equally well on lists of integers as on lists of reals or lists of strings. Futhermore, it allows one to write functions which take other functions as parameters. These are known as higher order functions and they give a second form of code re-use. There are powerful mechanisms for introducing user-defined datatypes such as trees, sets, graphic objects, etc. Haskell also makes a great deal of use of recursion. The combination of these features makes for very clean, short programs, which, with some experience, are easier to understand than many imperative programs.
In this course you will learn how to program in Haskell, which exemplifies the functional style, and also learn a little of the ideas on which functional programming is founded.
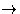a2
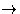a3 ... 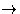an. Booleans and guards;
correspondence of guards with if-then-else expressions. Pairs and
n-tuples; fst and snd functions for dismantling pairs and
tuples. Pattern matching and cases, especially defining functions on
lists and tuples. Numeric calculation. Simple recursion, with
examples on the natural numbers and lists; list comprehension; list
processing examples which use patterns, recursion and comprehensions.
Evaluation, reduction strategies (such as eager and lazy), equational
reasoning. Type inference, basic types, higher types and type
variables; informal explanation of the Milner/Damas type inference
algorithm; methods for calculating types of expressions and declared
functions. Higher-order functions, polymorphism and code re-use;
examples such as the reversal of a list. Mathematical induction and
list induction: explanation of the basic principles, together with
examples of their application. New datatypes such as error types and
exception handling and declared datatypes; recursively defined
datatypes. Examples such as lists and trees. An introduction to
lexical analysis, parsing and pretty printing. Use of datatypes in
defining parsing tools and the (syntax tree) expressions of a
programming language. In depth account of parsing combinators. An
example parser.
S. Thompson, Haskell: The Craft of Functional Programming, Addison-Wesley 1996.
R. Bird and P. Wadler, Introduction to Functional Programming, Prentice Hall 1988.
L. Paulson, ML for the Working Programmer, 2nd Edition, CUP 1997.
The written January examination contains six questions, and candidates can obtain full marks from four good questions. The examination will test both the theoretical aspects of the course, as well as the ability to understand, analyse and write small programs.