[The University of Leicester]

Department of Mathematics & Computer Science



Next: MC395 Software Measurement and Quality Assurance Up: Year 3 Previous: MC383 Complex Analysis

MC384 Stochastic Modelling

MC384 Stochastic Modelling

Credits: 20 Convenor: Dr. M.J. Phillips Semester: 2
Prerequisites: essential: MC127, MC160, MC260, MC262, MC265
Assessment: Coursework: 10% Three-hour examination: 90%
Lectures: 36 Problem Classes: 10
Tutorials: none Private Study: 104
Labs: none Seminars: none
Project: none Other: none
Surgeries: none Total: 150

Explanation of Pre-requisites

The modules MC160 and MC260 provide the core probability and distribution theory which form an essential prerequisite for this module. A number of disparate mathematical tools are also required, which include the solution of simple differential/difference equations, and results from linear algebra and analysis. Courses which may cover these topics have not been included as prerequisites; a brief and informal description of the necessary tools and results are included when appropriate.

Course Description

In earlier courses we were mainly concerned with sequences of independent observations. Thus in a sequence of Bernoulli trials, the probabilities of success and failure remain constant, and the outcomes of successive trials are independent. In this module, we study random processes which somehow evolve in time. In general, the probability distribution among outcomes at some time t, now depends on the outcomes of the process at earlier times. For example, as a simple generalisation of Bernoulli trials, we might allow the probabilities of success and failure at the nth trial be governed by the outcome at the previous trial; this provides us with a simple two-state Markov chain (named after the Russian mathematician A. A. Markov who used this idea to model the alternation of vowels and consonants in a poem by Pushkin). This process and its extension to many states and more general time domains; the Markov process, provides a rich variety of models which have been applied in diverse areas such as; the biological sciences, including medicine; economic and financial modelling; engineering and the physical sciences; the social sciences and queuing theory.

The emphasis of the course is on encouraging probabilistic intuition and insight, and developing problem solving skills. A solid body of theory is covered (together with formal proofs where appropriate), but in the main the probabilistic content of results, and their application to problem solving, is stressed over analytical detail and proof.

Aims

To provide a body of core knowledge for probability modelling and basic stochastic processes. In particular, to provide a solid grounding in Markov processes, including the random walk and simple branching process; the Poisson and related processes, including the birth-death process and simple models for queuing theory; an introduction to the renewal process. To enhance the student's probabilistic insight and problem solving skills.

Objectives

On completion of this module, students should:

Transferable Skills

Syllabus

Review of some aspects of probability theory; the Total Probability Theorem, generating functions, random sums, limit theorems, the solution of difference equations. Basic concepts of a stochastic process; examples. Markov processes: Chapman-Kolmogorov equation. Markov chains; transition probability matrices; n-step transition probabilities; forward and backward equations; unconditional probabilities. Two-state Markov chain, limiting distribution, mean recurrence time. Classification of states; definition of terms irreducible, closed, absorbing, ephemeral, transient, recurrent, positive and null recurrent, period and ergodic. Basic Limit theorems; the decomposition theorems. Limiting distributions and the classification of states; examples to include the simple random walk with reflecting barrier. Absorption probabilities, mean time to absorption. Periodic chains. The simple branching process; mean and variance of the size of the nth generation, extinction probabilities.

The Poisson process; time to first and 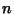$n$th events; times between events, the Markov property. Generalisations to two or more dimensions, the non-homogeneous Poisson process. Exponential waiting times, and other characterisations of the Poisson process. Modelling general lifetimes; hazard and reliability functions, the reliability of complex systems. The birth-death process; alternative specifications of particular forms, linear birth/death, immigration/emigration; examples to include solution of the immigration-linear-death process. Limiting distributions and the general birth-death process. A introduction to queuing theory.

An introduction to the renewal process; some basic limit distributions. Stopping times and Wald's Equation, a waiting time paradox. An application to queues.

Reading list

Background:

D. R. Cox and H. D. Miller, The Theory of Stochastic Processes, Chapman and Hall, 1997. S. Ross, Stochastic Processes, J. Wiley, 1996.. H. M. Taylor and S. Karlin, An Introduction to Stochastic Modelling, Academic Press, 1984.. H. C. Tuckwell, Elementary Applications of Probability Theory, Chapman and Hall, 1988..


Details of Assessment

The final assessment of this module will consist of 10% coursework and 90% from a three hour examination. The coursework contribution will be determined by students' solutions to coursework problems.

Next: MC395 Software Measurement and Quality Assurance Up: Year 3 Previous: MC383 Complex Analysis

[University Home] [MCS Home] [University Index A-Z] [University Search] [University Help]

Author: S. J. Ambler, tel: +44 (0)116 252 3884
Last updated: 2001-09-20
MCS Web Maintainer
This document has been approved by the Head of Department.
© University of Leicester.