![[The University of Leicester]](http://www.le.ac.uk/corporateid/departmentresource/000066/unilogo.gif) | Department of Mathematics & Computer Science |
 |
Next: MC440 Commutative Algebra
Up: Year 4
Previous: Year 4
MC430 Approximation Theory
| Credits: 20 |
Convenor: Jeremy Levesley |
Semester: 1 |
| Prerequisites: |
essential: MC144, MC145, MC146, MC147, MC240, MC241 |
desirable: MC243 |
| Assessment: |
Continual assessment: 10% |
Three hour exam: 90% |
| Lectures: |
36 |
Problem Classes: |
10 |
| Tutorials: |
0 |
Private Study: |
104 |
| Labs: |
none |
Seminars: |
none |
| Project: |
none |
Other: |
none |
| Surgeries: |
none |
Total: |
150 |
Explanation of Pre-requisites
I will use some results from MC243 about best approximations. Also
since the main space under study will be an inner product space, again
material from MC243 will smooth the student's path to understanding. However,
it is not essential to have done MC243, which deals with abstract inner product
spaces, whereas we have a single concrete space in mind.
Course Description
The course will expound the elementary theory of wavelets. These objects are of
great importance in signal processing, and in the compression (and thus speedy
transmission of) signals. A major modern application is in the transmission of
signals for high resolution TV.
A wavelet can be thought of as a small wave. You will
already be familiar with the waves 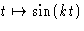 and
and 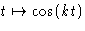 ,
where k is a whole number. These guys are pretty big waves in the sense of
modern wavelet theory. When they are used in signal processing, they are
naturally associated with the Fourier Series of the signal:
,
where k is a whole number. These guys are pretty big waves in the sense of
modern wavelet theory. When they are used in signal processing, they are
naturally associated with the Fourier Series of the signal:
![\begin{displaymath}
f(t) \approx (1/2)a_0 + \sum_{k=1}^\infty \Big[a_k\cos(kt) + b_k\sin(kt)\Big].
\end{displaymath}](img62.gif)
Over the years, mathematicians have struggled to understand in what senses the
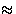 sign here can be replaced by =, and much famous theory has resulted
from this question. But it's not the fundamental one which a wavelet course
looks
at. Just suppose we have = in some suitable sense. If we then ask, ``Does the
signal contain significant amounts of frequency 136?", the answer is easy. The
frequency of the waves in the Fourier series is encoded via the index k, and
the amount of frequency 136 present in the signal f is governed by the size
of the numbers a136 and b136. If these numbers are (relatively) large,
frequency 136 will play a prominent role in the signal. A much harder question
is the analysis of the behaviour of the signal with the variable t, which is
usually indicating the progression of the signal over time. Are there times when
the signal is small? Are there times when the signal is slowly varying? Are
there times when the signal is large? rapidly varying? It's more or less
because
the
sign here can be replaced by =, and much famous theory has resulted
from this question. But it's not the fundamental one which a wavelet course
looks
at. Just suppose we have = in some suitable sense. If we then ask, ``Does the
signal contain significant amounts of frequency 136?", the answer is easy. The
frequency of the waves in the Fourier series is encoded via the index k, and
the amount of frequency 136 present in the signal f is governed by the size
of the numbers a136 and b136. If these numbers are (relatively) large,
frequency 136 will play a prominent role in the signal. A much harder question
is the analysis of the behaviour of the signal with the variable t, which is
usually indicating the progression of the signal over time. Are there times when
the signal is small? Are there times when the signal is slowly varying? Are
there times when the signal is large? rapidly varying? It's more or less
because
the 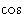 and
and 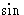 waves are somehow too big that these questions are tricky
to
answer. The course will show how to construct the most elementary wavelets, and
the famous decomposition and reconstruction algorithms for signals. Our main aim
will be to construct one of the famous wavelets due to Ingrid Daubechies from
scratch. This turns out to be a very tricky job, calling for some quite
sophisticated mathematics!
waves are somehow too big that these questions are tricky
to
answer. The course will show how to construct the most elementary wavelets, and
the famous decomposition and reconstruction algorithms for signals. Our main aim
will be to construct one of the famous wavelets due to Ingrid Daubechies from
scratch. This turns out to be a very tricky job, calling for some quite
sophisticated mathematics!
Aims
To understand the concept of a wavelet and appreciate how to construct the most
elementary wavelets. To understand the principles behind the reconstruction and
decomposition algorithms.
Objectives
Students will poseess the necessary theoretical understanding to construct the
Daubechies compactly supported wavelets. They will be able to write a computer
programme to implement the reconstruction and
decomposition algorithms. They will have gained knowledge of and experience with
working with the Fourier transform in a formal way.
Transferable Skills
Students will expand their ability to apply mathematics to practical
situations, and will also have considerable exposure to the Fourier transform.
Syllabus
The basic space L2(R) and the basic facts we need to know about it. Results
about the Fourier transform, including Parseval's identity. Brief discussion of
Fourier series. Introduction to wavelets, the Haar wavelet as an elementary
model example, the two-scale equation, multiresolution analysis, how the
multiresolution analysis aids the construction of wavelets, stable bases in
L2(R), the decomposition and reconstruction algorithms, the symbol,
compactly supported wavelets, the cascade algorithm for constructing wavelets
from the two scale equation, the Daubechies wavelets.
Reading list
Recommended:
C. Chui,
An Introduction to Wavelets,
Academic Press, 1992.
Background:
C. Chui, Chapter 1 in,
Advances in Numerical Analysis, Volume II: Wavelets, subdivision
algorithms and radial functions (ed W. Light),
OUP 1992.
Details of Assessment
The coursework for the continual assessment consists of about 8 pieces of
written work, consisting of problems from the problem sheets.
The written January examination lasts for three hours, and contains 6 questions.
Students must answer four.
Next: MC440 Commutative Algebra
Up: Year 4
Previous: Year 4
Author: S. J. Ambler, tel: +44 (0)116 252 3884
Last updated: 10/4/2000
MCS Web Maintainer
This document has been approved by the Head of Department.
© University of Leicester.
![[The University of Leicester]](http://www.le.ac.uk/corporateid/departmentresource/000066/unilogo.gif)
![[The University of Leicester]](http://www.le.ac.uk/corporateid/departmentresource/000066/unilogo.gif)
![]() and
and ![]() ,
where k is a whole number. These guys are pretty big waves in the sense of
modern wavelet theory. When they are used in signal processing, they are
naturally associated with the Fourier Series of the signal:
,
where k is a whole number. These guys are pretty big waves in the sense of
modern wavelet theory. When they are used in signal processing, they are
naturally associated with the Fourier Series of the signal:
![\begin{displaymath}
f(t) \approx (1/2)a_0 + \sum_{k=1}^\infty \Big[a_k\cos(kt) + b_k\sin(kt)\Big].
\end{displaymath}](img62.gif)