[The University of Leicester]

Department of Mathematics & Computer Science



Next: MC342 History of mathematics Up: Year 3 Previous: MC316 Parallel and Distributed Computing

MC341 Group Theory

MC341 Group Theory

Credits: 20 Convenor: Dr. R. Marsh Semester: 2

Prerequisites: essential: MC242
Assessment: Coursework: 10% Three hour exam: 90%

Lectures: 36 Problem Classes: 10
Tutorials: none Private Study: 104
Labs: none Seminars: none
Project: none Other: none
Surgeries: none Total: 150

Explanation of Pre-requisites

This module builds on the module MC242, Introduction to Groups, by developing the theory of groups; therefore it is essential that students are familiar with the content of MC242, although a brief revision of the material from MC242 will take place at the start of the course.

Course Description

This module builds upon MC242 (Introduction to Groups) and gives an overview of the main ideas of group theory. The emphasis is on structure theorems, classification results and decomposition concepts that have evolved as a result of attempts to describe all possible groups. Although such a description is not actually feasible, it is possible to obtain surprisingly detailed information about the structure of large classes of groups.

One of the major goals of the module is to develop enough theory to be able to discuss the classification of the finite simple groups, at least in broad general terms. This classification ranks as one of the major achievements in pure mathematics. Its proof runs to somewhere between 10,000 and 15,000 journal pages, spread across some 500 separate articles by more than 100 mathematicians, almost all written between 1950 and the early 1980's. A revision is currently underway, but even this is expected to run to more than 5,000 pages.

The module is designed to present a broad outline of the classification, to explain its significance, and to give a hint of the complexity of its proof.

Aims

This course aims to present the fundamental ideas of group theory by studying the structure theorems and decomposition concepts that arise in attempts to understand groups in terms of less complicated groups. These attempts are most successful in studying finite groups because there is a sense in which any finite group can be regarded as a group built from finite simple groups. The course aims to develop the ideas necessary to make this notion precise and to develop the theory needed to present a rough idea of the statement of the classification of finite simple groups.

Objectives

By the end of this module students should have developed an understanding of

Transferable Skills

This module should help the student develop a good sense of the axiomatic approach to mathematics. In addition, it provides students with practice in presenting reasoned arguments with precision and cogency.

Syllabus

Definition and examples of groups; the symmetric group and cycle decomposition of elements; free groups; subgroups; centralisers; centre of a group; products of subsets; cosets; Lagrange's Theorem; conjugates and conjugacy classes of elements and of subsets; normal subgroups; normalisers; quotient groups; homomorphisms and isomorphisms; kernels and images; the isomorphism theorems; normal closures; presentations of groups; generators and relations; direct products; automorphism groups and the conjugation map;

G-sets and actions; the kernel of an action; faithful and transitive actions; multiplication and conjugation actions; stabilisers and orbits; the Orbit-Stabiliser Theorem; the fixed point theorem for the number of orbits of an action; use of this theorem for enumeration. the alternating groups An; Cayley's theorem that every group is isomorphic to a subgroup of a symmetric group;

Sylow subgroups of finite groups; the Sylow theorems; characteristic subgroups; simple groups; normal and subnormal series; composition series and chief series; the Jordan-Hölder Theorem; solvable and nilpotent groups; commutator subgroups; upper and lower central series; derived series; that a finite p-group is nilpotent; normalisers in nilpotent groups; characterisation of nilpotent groups; simplicity of the alternating groups An for 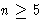$n\ge 5$;outline of the classification of finite simple groups.

Reading list

Recommended:

J. F. Humphreys, A Course in Group Theory, Oxford University Press.

Background:

J. A. Gallian, Contemporary Abstract Algebra, DC Heath.

D. Gorenstein, R. Lyons and R. Solomon, The classification of the finite simple groups, Mathematical Surveys and Monographs, 40.1. American Mathematical Society.

D. L. Johnson, Presentations of Groups, Cambridge University Press.

C. R. Jordan and D. A. Jordan, Groups, Edward Arnold.

I. D. MacDonald, Theory of Groups, Oxford University Press.

J. S. Rose, A Course in Group Theory, Cambridge University Pres.

J. J. Rotman, An Introduction to the Theory of Groups, Springer-Verlag.

Details of Assessment

There will be around 8 pieces of work set for assessment which will together count for 10% of the final mark; the final examination contributes the remaining 90%.

The exam paper contains 8 questions. Any number of questions may be attempted, but only the best 5 answers will be taken into account. Full marks may be obtained for answers to 5 questions. All questions carry equal weight.

Next: MC342 History of mathematics Up: Year 3 Previous: MC316 Parallel and Distributed Computing

[University Home] [MCS Home] [University Index A-Z] [University Search] [University Help]

Author: S. J. Ambler, tel: +44 (0)116 252 3884
Last updated: 10/4/2000
MCS Web Maintainer
This document has been approved by the Head of Department.
© University of Leicester.