[The University of Leicester]

Department of Mathematics & Computer Science



Next: MC248 Further Real Analysis Up: Year 2 Previous: MC243 Aspects of Linear Analysis

MC244 Geometry

MC244 Geometry

Credits: 10 Convenor: Dr. J.F. Watters Semester: 1 (weeks 7 to 12)

Prerequisites: essential: MC144, MC145, MC147
Assessment: Coursework: 20% One and a half hour exam in January: 80%

Lectures: 18 Problem Classes: 5
Tutorials: none Private Study: 52
Labs: none Seminars: none
Project: none Other: none
Surgeries: none Total: 75

Explanation of Pre-requisites

The module MC144 provides the mapping terminology and ideas, e.g. bijection, whilst MC145 covers the basic work on complex numbers used in this module. A number of examples of groups arise in this module and that concept is introduced in MC145. Module MC147 discusses matrices and these are used here to define mappings with invertible matrices being particularly significant.

Course Description

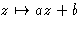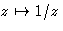The course covers four main topics. Isometries and similarities of the Euclidean (complex) plane are defined, classified, and represented by mappings, e.g. of the form $z \mapsto az + b$. The extended complex plane (inversive plane) is defined and properties of bilinear transformations, e.g. mappings of the sort $z \mapsto 1/z$, are explored using stereographic projection. The final topic is a brief discussion of the affine plane using matrices and here the basic idea is to examine mappings of the plane which are required simply to map lines to lines.

Aims

This module provides concrete examples of mappings and so aims to deepen understanding of the concept. It also provides examples of classification and invariants so giving experience of these approaches to mathematical ideas. Through exercises and examples the module shows how transformations can be used to solve geometrical problems. The module aims to develop the group concept through specific examples. Another main aim of the module is to provide an opportunity to increase the facility to work with complex numbers and to look at some elementary complex functions. Finally, using affine transformations the module examines affine properties of the plane and deals with the affine classification of conics.

Objectives

To identify transformations in Euclidean and non-Euclidean plane geometries.

To construct transformations with specific properties.

To be familiar with some geometric invariants of groups of transformations of the plane.

To understand stereographic projection and its mapping properties.

To have an understanding of bilinear transformations of the extended complex plane.

To use transformations to solve geometric problems.

To be able to identify the affine nature of a conic.

Transferable Skills

Developing facility to work with complex numbers.

Developing understanding of mappings and some group-theoretical ideas.

Transformation as a problem solving technique.

Written presentation of logical argument in geometric settings.

Syllabus

Basic complex algebra.

Isometries as transformations of the complex plane; products of reflections; properties invariant under isometries; classification of isometries. Apply isometric transformations to solve geometric construction problems.

Similarities as transformations of the complex plane; properties invariant under similarities; classification of similarities. Apply similarity transformations to solve geometric construction problems. Define and recognise groups of similarities (isometries).

Define inversion and bilinear transformations of the complex plane; stereographic projection and the extended complex plane; properties invariant under bilinear transformations (e.g. cross-ratio). Apply inversion to solve geometric construction problems.

Define affine transformations of the plane; properties invariant under affine transformations (e.g. ratio). Obtain affine equivalent forms of conics.

Reading list

Recommended:

H. S. M. Coxeter, Introduction to Geometry, 2nd edition, Wiley.

M. Jeger, Transformation Geometry, Allen and Unwin.

P. J. Ryan, Euclidean and Non-Euclidean Geometry - an Analytic Approach, Cambridge University Press.

Details of Assessment

Coursework will be set weekly and marks gained will provide the coursework component for assessment 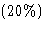$(20\%)$.Examination - one and a half hours duration with four questions, all of equal weight, three to be answered for full marks.

Next: MC248 Further Real Analysis Up: Year 2 Previous: MC243 Aspects of Linear Analysis

[University Home] [MCS Home] [University Index A-Z] [University Search] [University Help]

Author: S. J. Ambler, tel: +44 (0)116 252 3884
Last updated: 10/4/2000
MCS Web Maintainer
This document has been approved by the Head of Department.
© University of Leicester.