![[The University of Leicester]](http://www.le.ac.uk/corporateid/departmentresource/000066/unilogo.gif) | Department of Mathematics |
 |
Next: MA4501 Mathematics Project
Up: ModuleGuide03-04
Previous: MA4151 Lie Algebras
MA4161 Galois Theory
| Credits: 20 |
Convenor: Prof. S. König |
Semester: 2 |
| Prerequisites: |
essential: MC241, MC255 |
desirable: MC382 |
| Assessment: |
Coursework: 10% |
Three hour examination in June: 90% |
| Lectures: |
36 |
Problem Classes: |
10 |
| Tutorials: |
none |
Private Study: |
104 |
| Labs: |
none |
Seminars: |
none |
| Project: |
none |
Other: |
none |
| Surgeries: |
none |
Total: |
150 |
Subject Knowledge
Aims
To help the student to develop an appreciation of the rigorous development
of this beautiful subject, and an understanding of the fundamental results
of the subject.
Learning Outcomes
To enable the student to :
Understand and define the Galois group of a field extension, and the Galois
group of a polynomial.
Understand and prove the Galois correspondence, including the relationship
between the normal subject structure of the Galois group and normality of
intermediate extensions.
Understand the definition of a solvable group and be able to determine whether
or not a group of reasonable size is solvable.
Appreciate the significance of the Galois group of a polynomial as a group of
permutations of the roots.
Prove that the alternating group of degree at least 5 is simple.
Understand the definition of a radical extension and prove that such an extension
has a solvable Galois group.
Understand Lagrange resolvents and their use in proving that a finite separable
normal extension with a solvable Galois group is a radical extension.
Understand that the symmetric group is the Galois group of the general polynomial.
Be able to construct polynomials whose Galois group is not solvable.
Subject Skills
Aims
This course should assist the student to develop skills of careful and
rigorous Mathematcial writing and expression. It could also serve as
preparation for s student wishing to embark on research in Pure Mathematics,
as it should convey an appreciation of a common strand of development in
modern Mathematics.
Explanation of Pre-requisites
It will be assumed that the student has some familiarity with the basic
properties of groups, and knows the beginnings of the theory of field
extensions. It would be desirable, but is not essential, for the student
to have seen the definition of a solvable group.
Course Description
Galois theory is one of the first examples of methods from one branch of
Mathematics being applied to solve problems in an apparently completely
different area. Which regular 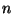 -sided polygon can be constructed by ruler
and compass? For a specific
-sided polygon can be constructed by ruler
and compass? For a specific 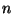 , such a question can be given a positive
answer by finding an explicit construction. But how does one prove that
there is no such construction for certain
, such a question can be given a positive
answer by finding an explicit construction. But how does one prove that
there is no such construction for certain 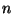 ? And what is the difference
between
? And what is the difference
between 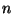 's for which there is a construction and
's for which there is a construction and 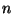 's for which
there isn't?
's for which
there isn't?
Surprisingly, this question is closely related to the problem of solving
polynomial equations by radicals, that is, finding a formula which only
involves the coefficients of the polynomial and arithmetic operations
including taking roots. Everybody knows the answer for polynomials of
degree two. But what happens in general? Again, for a specific 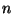 one may
give a positive answer by finding an explicit formula. But how does one
prove that there is no such formula for certain
one may
give a positive answer by finding an explicit formula. But how does one
prove that there is no such formula for certain 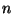 ?
?
This course will provide complete anwers to both problems by transforming
them into questions about algebraic structures such as groups and fields.
The main theorem of Galois theory is one of the most beautiful theorems in
all of mathematics, and extensions and applications of Galois theory are the
subject of major research activities in algebra, geometry and analysis.
Syllabus
Automorphisms of field extensions. The Galois group of a finite extension.
Normal extensions. Separability. The Galois correspondence. The Galois group
of a polynomial, viewed as a group of permutations of the roots. Transitivity
of the Galois group of an irreducible polynomial on the roots. Composition
series for groups and characterization of solvable groups in terms of these.
Alternating groups and proof of their simplicity in degree greater than 4.
Radical extensions and the solvability of their Galois groups. Lagrange
resolvents and the proof that a radical normal extension has a solvable Galois
group. The symmetric group as the Galois group of the ``general''polynomial.
Explicit determination of the general solution of the general cubic and quartic.
Examples of polynomials which are not solvable by radicals.
Reading list
Background:
P.M.Cohn,
Algebra II,
S.Lang,
Algebra,
J. Rotman,
Galois Theory,
I. Stewart,
Galois Theory,
Chapman and Hall.
Module Evaluation
Module questionnaires, module review, year review.
Next: MA4501 Mathematics Project
Up: ModuleGuide03-04
Previous: MA4151 Lie Algebras
Author: C. D. Coman, tel: +44 (0)116 252 3902
Last updated: 2004-02-21
MCS Web Maintainer
This document has been approved by the Head of Department.
© University of Leicester.
![[The University of Leicester]](http://www.le.ac.uk/corporateid/departmentresource/000066/unilogo.gif)
![[The University of Leicester]](http://www.le.ac.uk/corporateid/departmentresource/000066/unilogo.gif)
![]() one may
give a positive answer by finding an explicit formula. But how does one
prove that there is no such formula for certain
one may
give a positive answer by finding an explicit formula. But how does one
prove that there is no such formula for certain ![]() ?
?