[The University of Leicester]

Department of Mathematics



Next: MA2161 Algebra II Up: ModuleGuide03-04 Previous: MA2121 Linear Analysis

MA2151 Abstract Analysis

MA2151 Abstract Analysis

Credits: 10 Convenor: Prof. J.R. Hunton Semester: 2 (weeks 15 to 26)
Prerequisites: essential: MA1151, MA2101
Assessment: Coursework: 20% Examination: 80%
Lectures: 18 Problem Classes: 5
Tutorials: none Private Study: 46
Labs: none Seminars: none
Project: none Other: none
Surgeries: 6 Total: 75

Subject Knowledge

Aims

This module aims to free the ideas of continuity and integration from the boring old straight line to more interesting geometric and other mathematical objects.

Learning Outcomes

Students will see some classical examples of how a mathematical idea developed in one context can be reworked to apply to a lot of different situations. Explicitly, they will know the elementary stages of the study of metric, toplogical and measure spaces and the modern theory of integration, linked by a common flow of ideas.

Methods

Lectures, example classes, example sheets, surgeries.

Assessment

Marked problem sheets, written examination.

Subject Skills

Aims

To see how one can abstract a simple idea in one field of mathematics and develop it to a useful tool in many others.

Learning Outcomes

Students will learn how the idea of distance on the real line is developed to the idea of a metric on a general set, and how the study of continuity in this setting leads to the idea of a topological space. A similar flow of ideas leads from the inadequacy of Riemann integration to the elementary concepts of measure theory and Lebesque integration. Students will develop skills in presenting and understanding arguments in an abstract setting and in the ability to construct logical arguments.

Methods

Lectures, examples classes, example sheets, surgeries.

Assessment

Marked problem sheets, written examination.

Explanation of Pre-requisites

This module takes the ideas seen in the first two analysis modules and starts them over again in a more general and more applicable setting. Basic familiarity with main ideas from the two earlier modules will be assumed.

Course Description

For many thousands of years mathematicians have developed their subject as a way to understand and describe the world around them, through geometry, number and physical theories. Two of the main intuitive ideas have been the concepts of measurement and proximity. Rigorous treatments of these ideas in modern guise led to the theories of continuity and integration seen in earlier modules, but these are inadequate in a number of ways. For one, matheamticians deal with more things than just the real line, and the geometry of the world (let alone of space-time or of the quantum universe) is richer than can be found by studying just one dimension. This module sits a a cross-roads between the classical analysis of the real line already seen in earlier modules, and the modern developments seen in the third and fourth level modules covering divers topics such as Topology, Geometry, Approximation Theory, Dynamics, and so on.

Syllabus

Metric spaces, continuity via balls and via open sets; lack of accumulation points in an infinite set leading to ideas of completeness and compactness. Heine-Borel and corollaries. Topological spaces and compactness again. Sub- and quotient-spaces. Measure spaces, 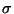$\sigma$-algebras and measurable functions. Lebesgue measure; integration and Lebesgue monotone convergence theorem.

Reading list

Recommended:

Essential:

W. A. Sutherland, Introduction to metric and topological spaces, Oxford : Clarendon Press, 1975.

W. Rudin, Real and Complex Analysis, McGraw Hill, 1970.

Background:

Resources

Problem sheets, lecture and surgery rooms, lecturer.

Module Evaluation

Module questionnaires, module review, year review.

Next: MA2161 Algebra II Up: ModuleGuide03-04 Previous: MA2121 Linear Analysis

[University Home] [MCS Home] [University Index A-Z] [University Search] [University Help]

Author: C. D. Coman, tel: +44 (0)116 252 3902
Last updated: 2004-02-21
MCS Web Maintainer
This document has been approved by the Head of Department.
© University of Leicester.