![[The University of Leicester]](http://www.le.ac.uk/corporateid/departmentresource/000066/unilogo.gif) | Department of Mathematics |
 |
Next: MA1102 Algebraic Structures and Number Systems
Up: ModuleGuide03-04
Previous: MA1061 Probability
MA1101 Proof and Logical Structures
| Credits: 10 |
Convenor: Prof. J.R. Hunton |
Semester: 1 (weeks 1 to 6) |
| Prerequisites: |
|
|
| Assessment: |
Coursework: 20% |
Examination: 80% |
| Lectures: |
18 |
Problem Classes: |
6 |
| Tutorials: |
none |
Private Study: |
45 |
| Labs: |
none |
Seminars: |
none |
| Project: |
none |
Other: |
none |
| Surgeries: |
6 |
Total: |
75 |
Subject Knowledge
Aims
This module aims to introduce the student to rigorous university level
mathematics. It discusses the need for and nature of Proof and the types
of logical argument used in a Mathematics degree. In the process a number
of basic terms, symbols and ideas are developed.
Learning Outcomes
Students will know the standard types of mathematical proof - direct
proofs, proofs by cases, proof by contradiction and by contrapositive,
proof by induction. Students will also know some simple and some classical
examples of proofs, such as the irrationality of 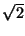 and the
existence of an infinite number of primes, and be able to present and
construct some simple proofs themselves. Students will be familar also
with the need for careful definition of concepts and the careful statement
of mathematical results. They will have some facility at the formation of
the negation of statements. They will also be familar with a number of
basic pieces of mathematical language and symbol, including that of
functions and equivalence relations.
and the
existence of an infinite number of primes, and be able to present and
construct some simple proofs themselves. Students will be familar also
with the need for careful definition of concepts and the careful statement
of mathematical results. They will have some facility at the formation of
the negation of statements. They will also be familar with a number of
basic pieces of mathematical language and symbol, including that of
functions and equivalence relations.
Methods
Lectures, supervisions, example sheets and class tests, surgeries.
Assessment
Marked problem sheets, class tests, written examination.
Subject Skills
Aims
To develop students' critical understanding of mathematical method
and written communication skills.
Learning Outcomes
Students will have familiarity with the stardard types of mathematical
argument, be able to reproduce and manipulate definitions, statements and
arguments with precision, recognising the need for such precision and be
able to present written arguments in a coherent and logical form.
Methods
Lectures, supervisions, example sheets and class tests, surgeries.
Assessment
Marked problem sheets, class tests, written examination.
Explanation of Pre-requisites
This module is a first mathematics module and makes no use of other
modules. Some familiarity with higher level
school mathematics will be assumed.
Course Description
This module is intended to help students understand what consitutes a
proper mathematical statement and proof, and why one needs these concepts
and level of precision. It aims to introduce the need for mathematical
argument through the unfamilar world of counting infinite numbers and
proceeds to look at the standard types of mathematical argument and
language used. In the process a number of very simple and familar ideas
are worked through, as are a couple of classical arguments from antiquity
- the irrationality of 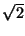 and the infinite number of primes. This
module also allows the development of a number of pieces of mathemtical
terminology used throughout the degree - the ideas of function and
equivalence relation, for example. A small amount of set theoretic
language is introduced and used.
and the infinite number of primes. This
module also allows the development of a number of pieces of mathemtical
terminology used throughout the degree - the ideas of function and
equivalence relation, for example. A small amount of set theoretic
language is introduced and used.
Syllabus
The idea of and need for mathematical statements and proofs. Direct
proofs, proofs by cases, proof by contradiction, proof by contrapositive,
proof by induction. The irrationality of 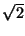 , the infinite number
of primes. Discussion of negations and logical connectives (and, or, not,
implies, iff). Discussion of familar examples such as
, the infinite number
of primes. Discussion of negations and logical connectives (and, or, not,
implies, iff). Discussion of familar examples such as 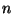 even if and only
if
even if and only
if 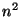 even. Functions and the properties of being 1-1, onto or
bijective; equivalence relations.
even. Functions and the properties of being 1-1, onto or
bijective; equivalence relations.
Reading list
Recommended:
P.J. Eccles,
An Introduction to Mathematical Reasoning,
Cambridge University Press.
Background:
N. L. Biggs,
Discrete Mathematics,
Oxford University Press.
P. M. Cohn,
Algebra I,
John Wiley.
D. Driscoll Schwartz,
Conjecture and proof,
Harcourt Brace.
S. Galovich,
Doing Mathematics,
Harcourt Brace.
R. Garnier and J. Taylor,
100% Mathematical Proof,
John Wiley.
A. G. Hamilton,
Numbers, Sets and Axioms,
Cambridge University Press.
G. Pólya,
How to Solve It,
Penguin.
S. Singh,
Fermat's Last Theorem,
Fourth Estate.
D. Solow,
How to Read and Do Proofs
I. Stewart and D. Tall,
The Foundations of Mathematics,
Oxford University Press.
D. J. Velleman,
How to Prove It,
Cambridge University Press.
Resources
Problem sheets, lecture rooms, surgeries and supervision rooms. Human
resources.
Module Evaluation
Module questionnaires, module review, year review.
Next: MA1102 Algebraic Structures and Number Systems
Up: ModuleGuide03-04
Previous: MA1061 Probability
Author: C. D. Coman, tel: +44 (0)116 252 3902
Last updated: 2004-02-21
MCS Web Maintainer
This document has been approved by the Head of Department.
© University of Leicester.
![[The University of Leicester]](http://www.le.ac.uk/corporateid/departmentresource/000066/unilogo.gif)
![[The University of Leicester]](http://www.le.ac.uk/corporateid/departmentresource/000066/unilogo.gif)