![[The University of Leicester]](http://www.le.ac.uk/corporateid/departmentresource/000066/unilogo.gif) | Department of Mathematics & Computer Science |
 |
Next: MA1271 Geometry of the Plane
Up: Level 1
Previous: MA1221 Pure Mathematics at Work
MA1251(=MC183) Chaos and Fractals
| Credits: 10 |
Convenor: Dr Ruslan Davidchack |
Semester: 2 |
| Prerequisites: |
essential: None |
desirable: |
| Assessment: |
Continual assessment: (30% coursework problems, 70%
lab reports) 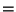 100%% 100%% |
Examination: 0% |
| Lectures: |
6 |
Problem Classes: |
none |
| Tutorials: |
6 |
Private Study: |
51 |
| Labs: |
12 |
Seminars: |
0 |
| Project: |
none |
Other: |
none |
| Surgeries: |
none |
Total: |
75 |
Course Description
The extraordinary visual beauty of fractal images and their applications
in chaos theory have made these endlessly repeating geometric figures
widely familiar. Yet they are more than just appealing visual patterns
and have proved to have wide range of uses.
Chaos dynamics and fractal geometry are important and exciting topics
in contemporary mathematics. This course introduces these topics using
a combination of hands-on computer experimentation and simple
mathematics. Students are led through a series of experiments that
produce fascinating images of Julia sets, Mandelbrot sets, and
fractals. The basic ideas of dynamics - iteration, stability, and
chaos - are illustrated via computer projects.
Aims
To present an overview of the exciting area of nonlinear
dynamical systems at a level accessible to first year undergraduates.
Objectives
Understand basic concepts of the theory of dynamical systems.
Know typical mechanisms by which simple systems generate
complicated dynamics and fractal structures.
Develop skills for modelling simple dynamical systems and
studying their properties.
Transferable Skills
Use of the scientific computing environment MATLAB, modelling skills.
Syllabus
Dynamical systems. Orbits. Fixed and periodic points.
Graphical analysis. The logistic function.
Stable and unstable orbits. Chaotic orbits. Sensitive dependence on
initial conditions. Lyapunov exponent.
Period doubling bifurcation. Bifurcation diagrams.
Self-similarity and fractals. Cantor sets. Constructing fractals.
Fractal dimension. Julia sets. Parameter spaces and Mandelbrot sets.
Fractal basins of the Newton-Raphson method.
Reading list
Recommended:
R. L. Devaney,
Chaos, Fractals, and Dynamics: Computer Experiments in Mathematics,
Addison-Wesley.
H. Lauwerier,
Fractals: Enlessly Repeated Geometrical Figures,
Penguin Books.
P. S. Addison,
Fractals and Chaos: an Illustrated Course,
Institute of Physics Publishing.
M. Barnsley,
Fractals Everywhere,
Academic Press.
B. Fraser,
The Non-Linear Lab,
http://www.apmaths.uwo.ca/~ bfraser/version1/nonlinearlab.html,
Details of Assessment
There is no examination for this module.
The module assessment will be as follows:
30% for a coursework problems and 70% for lab reports.
Next: MA1271 Geometry of the Plane
Up: Level 1
Previous: MA1221 Pure Mathematics at Work
Author: G. T. Laycock, tel: +44 (0)116 252 3902
Last updated: 2002-10-25
MCS Web Maintainer
This document has been approved by the Head of Department.
© University of Leicester.
![[The University of Leicester]](http://www.le.ac.uk/corporateid/departmentresource/000066/unilogo.gif)
![[The University of Leicester]](http://www.le.ac.uk/corporateid/departmentresource/000066/unilogo.gif)