	Department of Mathematics & Computer Science

Next: MA1101 Proof and Logical Structures Up: Level 1 Previous: MA1051 Newtonian dynamics

MA1061 Probability

MA1061(=MC160) Probability

Credits: 10

Convenor: Dr Jeremy Levesley

Semester: 2

Prerequisites:		desirable: MA1001(=MC126)
Assessment:	Coursework: two 30 minute tests.: 20%	One and a half hour examination.: 80%

Lectures:	18	Problem Classes:	none
Tutorials:	5	Private Study:	52
Labs:	none	Seminars:	none
Project:	none	Other:	none
Surgeries:	none	Total:	75

Explanation of Pre-requisites

There are few formal prerequisites beyond what is normally covered in

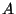-level mathematics syllabuses. Mathematical topics which may not appear in some syllabuses; for example the exponential series, are covered informally, and relevant results are stated. The module MA1001 provides the proofs of some calculus results which are used in this module, and introduces some basic multivariate calculus techniques which will be essential for later modules in probability and distribution theory.

Course Description

Probability statements are almost unavoidable, and probability models pervade most areas of science. This course introduces the basic ideas and rules of probability, together with some simple probability models and techniques for computing the probabilities of events.

We introduce the important concept of random variable (basically the summary of the outcome of an experiment in a single real number) together with its probability distribution or density function, its expectation and variance. A number of important distributions are introduced, including the binomial, geometric, Poisson and normal distributions. The course concludes with a statement of the Central Limit Theorem.

Emphasis is placed on those aspects of probability required in statistical inference; on developing a good intuitive grasp of basic concepts, and problem solving.

Aims

To develop a strong intuitive understanding of the basic ideas of probability, probability models, random variables and their distributions.

Although mathematical formality is kept to a minimum, the importance and advantages of carefully specifying events, random variables, and assumptions, together with a careful and reasoned application of basic rules, is stressed. Emphasis is very much on developing problem solving skills within a probabilistic setting.

Objectives

On completion of this module, students should:

$\bullet$: understand the basic interpretations of probability and simple rules;
$\bullet$: be able to compute probabilities for events defined on a sample space of equally likely sample points;
$\bullet$: understand the concept of random variable and the differences between discrete and continuous random variables;
$\bullet$: know what is meant by a probability distribution or probability density function; be able to apply the appropriate methods for computing probabilities, expectations and variances;
$\bullet$: understand the genesis of the binomial, geometric and Poisson distributions (details such as probability distribution and moments are not essential - they appear in standard tables);
$\bullet$: be aware of the normal distribution, its ubiquity, its parameters and their interpretation, the general shape of its probability density function, and finding probabilities using standard tables;
$\bullet$: know the rules for finding the mean and variance (for independent random variables) of linear combinations of random variables;
$\bullet$: understand the content and consequences of the DeMoivre-Laplace and Central Limit Theorems and be able to apply them to simple problems.

Transferable Skills

$\bullet$: An understanding of the concept of probability and the interpretation of simple probability statements.
$\bullet$: A reasonable grasp of the material covered in this module forms an essential prerequisite for all later courses in probability and statistics, or indeed any discipline employing probabilistic modelling.
$\bullet$: Development of problem solving skills; problem formulation and the presentation of a reasoned solution.

Syllabus

Interpretations of probability; the frequency and subjective interpretations. Role of probability in statistics. The axioms of probability, their motivation and some simple consequences. Simple combinatorial results; the evaluation of probabilities in models with equally likely outcomes. Conditional probability and independence. The Total Probability Theorem; Bayes' Theorem.

Random variables; discrete and continuous. Probability distributions, density functions and the distribution function. Expectations; the mean and variance. Basic distributions; binomial, geometric, Poisson and normal distributions. The Poisson distribution as a limiting binomial distribution. The DeMoivre-Laplace Limit Theorem.

Means and variances of linear combinations of independent random variables and normal variables; the Central Limit Theorem.

Reading list

Details of Assessment

The final assessment of this module will consist of 20% from two 30-minute class tests and 80% from a one and a half hour examination during the Summer exam period. The examination paper will contain 4 questions with full marks on the paper obtainable from 4 complete answers.