[The University of Leicester]

Department of Mathematics & Computer Science



Next: CO2011 Automata, Languages and Computation Up: Year 2 Previous: CO2006 Software Engineering and System Development

CO2008 Functional Programming

CO2008 Functional Programming

Credits: 20 Convenor: Dr. N. Ghani Semester: 1
Prerequisites: essential: CO1003, CO1004, CO1011
Assessment: Coursework: 50% Three hour exam in January: 50%
Lectures: 36 Problem Classes: none
Tutorials: none Private Study: 78
Labs: 24 Seminars: none
Project: none Other: none
Surgeries: 12 Total: 150

Subject Knowledge

Aims

The module will give the student a thorough grounding for programming in the functional style using the language Haskell.

Learning Outcomes

Students will be able to: develop skilled use of basic functions and techniques to solve problems in practical applications; understand and use polymorphism in designing functions which allow code re-use; understand the use of higher order functions in designing functions which allow code re-use; understand the basics of polymorphic type inference; understand Haskell's mechanism for defining new datatypes.

Methods

Class sessions together with lecture slides, recommended textbook, worksheets, printed solutions, and some additional hand-outs and web support.

Assessment

Marked coursework, traditional written examination.

Subject Skills

Aims

To teach students how to methodically solve problems given the techniques available to them.

Learning Outcomes

Students will be able to: produce a variety of work in different formats; breakdown a problem to identify essential elements; apply prior knowledge of subject to analyse problems; generate and evaluate a range of strategies to address a problem; design a plan to solve a problem; implement a planned solution and evaluate the implementation.

Methods

Class sessions together with worksheets.

Assessment

Marked coursework, traditional written examination.

Explanation of Pre-requisites

It is essential that students have taken a first course in basic (imperative) programming, which includes skills involving both coding and design, to a level which includes data structures such as lists and trees.

A grounding in the basic mathematical concepts of sets, functions and relations is required, but detailed knowledge of other areas of elementary discrete mathematics and logic is not essential.

Course Description

Many of the ideas used in imperative programming arose through necessity in the early days of computing when machines were much slower and had far less memory than they do today. Languages such as C(++) and Pascal carry a substantial legacy from the past. Even Java, despite its OO features, has been devised to look `a bit like C'. If one were to start again and design a programming language from scratch what would it look like?

For many applications, the chief concern should be to produce a language which is concise and elegant. It should be expressive enough for a programmer to work productively and efficiently but simple enough to minimize the chance of making serious errors. Rapid development requires the programmer to be able to write algorithms and data structures at a high level without worrying about the details of their machine-level implementation. These are some of the criteria which have led researchers to develop the functional programming language Haskell.

The flavour of programming in Haskell is very different from that in an imperative language. Much of the irrelevant detail has been swept away. For example, there are at least three different uses for a variable in Pascal: as a storage location, as parameter in a function or procedure, as a temporary name for another variable (a `var parameter'). There is only one use for a variable in Haskell: it stands for a quantity that you don't yet know, as is standard in mathematical practice. The constructs in Pascal include expressions, commands, functions and procedures (the last two are confused in C); whereas in Haskell there are only expressions and functions. The meaning of a program in Pascal or C is understood by the effect it has on the `state' of the machine as it runs. Haskell does away with the idea of `state' -- the meaning of a program is understood by the values it computes.

On the other hand, Haskell is a very expressive language. The type system allows functions to be written polymorphically so that the same code can be re-used on data of different types, e.g. the same length function works equally well on lists of integers as on lists of reals or lists of strings. Furthermore, it allows one to write functions which take other functions as parameters. These are known as higher order functions and they give a second form of code re-use. There are powerful mechanisms for introducing user-defined datatypes such as trees, sets, graphic objects, etc. Haskell also makes a great deal of use of recursion. The combination of these features makes for very clean, short programs, which, with some experience, are easier to understand than many imperative programs.

This course teaches how to program in Haskell, which exemplifies the functional style, and also a little of the ideas on which functional programming is founded.

Syllabus

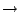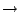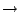Basic types, such as Int, Float, String, Bool; examples of expressions of these types. Functions and declarations, with a high level explanation of a function with general type a1 $\rightarrow$ a2 $\rightarrow$ a3 ... $\rightarrow$ an. Booleans and guards; correspondence of guards with if-then-else expressions. Pairs and n-tuples; fst and snd functions for dismantling pairs and tuples. Pattern matching and cases, especially defining functions on lists and tuples. Numeric calculation. Simple recursion, with examples on the natural numbers and lists; list comprehension; list processing examples which use patterns, recursion and comprehensions. Type inference, basic types, higher types and type variables; informal explanation of the Milner/Damas type inference algorithm; methods for calculating types of expressions and declared functions. Higher-order functions, polymorphism and code re-use; examples such as the reversal of a list. Mathematical induction and list induction: explanation of the basic principles, together with examples of their application. New datatypes such as error types and exception handling and declared datatypes; recursively defined datatypes. Examples such as lists and trees.

Reading list

Essential:

S. Thompson, Haskell: The Craft of Functional Programming, 2nd Edition, Addison-Wesley. 1999.

Recommended:

R. Bird and P. Wadler, Introduction to Functional Programming, Prentice Hall 1988.

Background:

L. Paulson, ML for the Working Programmer, 2nd Edition, CUP 1997.

Resources

Lecture slides, web page, study guide, worksheets, handouts, lecture rooms with two OHPs, past examination papers.

Module Evaluation

Course questionnaires, course review.

Next: CO2011 Automata, Languages and Computation Up: Year 2 Previous: CO2006 Software Engineering and System Development

[University Home] [MCS Home] [University Index A-Z] [University Search] [University Help]

Author: N. Rahman, tel: +44 (0)116 252 3902
Last updated: 2003-09-23
MCS Web Maintainer
This document has been approved by the Head of Department.
© University of Leicester.